!! used as default html header if there is none in the selected theme. OEF Cryptage RSA

OEF Cryptage RSA --- Introduction ---

Ce module regroupe pour l'instant 6 exercices sur le système de cryptologie RSA : création d'un système RSA, crypter/décripter un message, cryptanalyse.

Création RSA

Le but de cet exercice est de créer un système de cryptage RSA (de simulation).

Etape 1. Trouvez deux nombres premiers, et , tels que , . Calculez .

Vous avez pris , , .

Etape 2. Trouvez un entier alpha tel que l'application avec soit bijective sur l'ensemble d'éléments inversibles de . (Vous devez prendre 10000 alpha .)

Vous avez pris .

Etape 3. En utilisant comme clé publique d'un système de cryptage RSA, quelle est la clé privée, c'est-à-dire l'entier 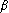beta tel que ?

Cryptage RSA

Le but de cet exercice est de simuler un cryptage RSA par clé publique.

Supposons que dans une communication sécurisée, votre interlocuteur vous a envoyé un couple comme clé publique d'un système RSA, où

,
.

Maintenant supposons que vous avez un message à envoyer. Ce message (d'origine) est représenté par le nombre suivant :

Quel est le message crypté correspondant que vous devez envoyer à votre interlocuteur ? (Ce dernier doit être un nombre compris entre 0 et N-1.)

Décrypt RSA

Le but de cet exercice est de décrypter un message sur un système de cryptage RSA donné (de simulation).

Nous avons deux nombres premiers, et . Soit

.

Prenons tel que le couple forme la clé publique d'un système RSA.

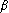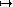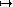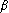Etape 1. Calculez la clé privée, c'est-à-dire l'entier beta tel que x mapsto soit la réciproque de x mapsto dans . (Parmi les choix de beta, vous devez prendre le plus petit entier positif.)

Oui, .

Etape 2. En utilisant la clé publique , votre interlocuteur vous a envoyé le message (nombre) crypté suivant. Quel est le message (nombre) d'origine ? (Ce dernier doit être un nombre compris entre 0 et N-1.)

Cryptanalyse RSA

Vous êtes en train d'écouter une communication ``sécurisée'' entre deux interlocuteurs inconnus. L'un d'eux utilise un système de cryptage RSA, avec clé publique

,
.

Vous vous appercevez que la clé n'est pas suffisamment longue, de sorte que vous pouvez décrypter les messages sans connaitre la clé privée, en utilisant les outils en ligne sur WIMS. Vous êtes tenté de le faire.

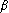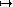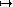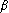Etape 1. Calculez la clé privée, c'est-à-dire l'entier beta tel que x mapsto soit la réciproque de x mapsto dans . (Parmi les choix de beta, il faut prendre le plus petit entier positif.)

Oui, .

Etape 2. Maintenant vous captez le message (nombre) crypté suivant. Quel est le message (nombre) d'origine ? (Ce dernier doit être un nombre compris entre 0 et N-1.)

Système de Diffie-Hellman

Vous avez choisi d'utiliser avec votre interlocuteur le système de Diffie-Hellman. Votre interlocuteur a choisi le nombre premier et le générateur de . Il vous a envoyé l'entier . Vous lui envoyez l'entier .

Le nombre est-il public ou privé ? Quel est ? Que vaut votre secret commun ?

Système de Diffie-Hellman 0

Vous avez choisi d'utiliser avec votre interlocuteur le système de Diffie-Hellman. Votre interlocuteur a choisi le nombre premier et le générateur de . Il a choisi un entier qu'il a gardé secret et vous a envoyé mod . Vous choisissez l'entier au hasard. Quel est votre secret commun ? The most recent version
Cette page n'est pas dans son apparence habituelle parce que WIMS n'a pas pu reconnaître votre navigateur web.
Afin de tester le navigateur que vous utilisez, veuillez taper le mot wims ici : puis appuyez sur ``Entrer''.

Veuillez noter que les pages WIMS sont générées interactivement; elles ne sont pas des fichiers HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE. Il est inutile pour vous de les ramasser par un programme robot.