Résolution numérique de l'équation f ( x ) = 0
Résolution numérique de l'équation f ( x ) = 0
- I Introduction
- II Méthode de dichotomie
- III Méthode de point fixe
- IV Méthode de Newton
- V Méthode de Lagrange
- VI Bibliographie
- VII Exercices
- Index
Ce document, destiné à des étudiants de L3, explique quelques méthodes permettant de trouver numériquement les zéros de fonctions d'une variable réelle.
Vous trouverez ici le fichier pdf doczero.pdf
I Introduction
Résolution numérique de l'équation f ( x ) = 0
→ I Introduction
I-1 Préambule
Résolution numérique de l'équation f ( x ) = 0
→
I Introduction
→ I-1 Préambule
- I Introduction
- II Méthode de dichotomie
- III Méthode de point fixe
- IV Méthode de Newton
- V Méthode de Lagrange
- VI Bibliographie
- VII Exercices
- Index
L'étude générale des fonctions à variables réelles nécessite de temps à autre la résolution d'équations de
type
f(x) = 0. Autrement dit, nous sommes amenés à trouver les zéros de fonctions non linéaires,
c'est-à-dire les valeurs réelles
 telles que
ou, ce qui est équivalent, à résoudre une équation
de type
telles que
ou, ce qui est équivalent, à résoudre une équation
de type
 telles que
telles que
I-2 Exemple motivant: équation d'état d'un gaz
Résolution numérique de l'équation f ( x ) = 0
→
I Introduction
→ I-2 Exemple motivant: équation d'état d'un gaz
- I Introduction
- II Méthode de dichotomie
- III Méthode de point fixe
- IV Méthode de Newton
- V Méthode de Lagrange
- VI Bibliographie
- VII Exercices
- Index
On veut déterminer le volume
V occupé par un gaz de température
T et de pression
p. L'équation
d'état (c'est-à-dire l'équation qui lie
p, V et
T) est :
où
a et
b sont deux coefficients dépendants de la nature du
gaz,
N le nombre de molécules contenues dans le volume
V et
k la constante de Boltzmann. Il faut donc résoudre une
équation non linéaire d'inconnue
V. Ceci revient à trouver
les zéros de la fonction :
Dans le cas le plus général, il s'agit de résoudre une équation non linéaire dont on n'est pas capable de trouver une solution exacte. Dans ce cas, on dispose de quelques méthodes numériques exécutables sur des logiciels comme Matlab, Maple, Octave, Scilab pour approximer la solution exacte. Ces méthodes numériques sont toutes basées sur la construction d'une suite convergeant vers un réel vérifiant
.
vérifiant
.
Dans ce document, nous allons traiter quatre méthodes: la méthode de dichotomie, de point fixe, de Newton et de Lagrange. Pour le faire, nous avons besoin de quelques rappels d'analyse.
Dans le cas le plus général, il s'agit de résoudre une équation non linéaire dont on n'est pas capable de trouver une solution exacte. Dans ce cas, on dispose de quelques méthodes numériques exécutables sur des logiciels comme Matlab, Maple, Octave, Scilab pour approximer la solution exacte. Ces méthodes numériques sont toutes basées sur la construction d'une suite convergeant vers un réel
 vérifiant
.
vérifiant
.Dans ce document, nous allons traiter quatre méthodes: la méthode de dichotomie, de point fixe, de Newton et de Lagrange. Pour le faire, nous avons besoin de quelques rappels d'analyse.
I-3 Rappels d'analyse
Résolution numérique de l'équation f ( x ) = 0
→
I Introduction
→ I-3 Rappels d'analyse
- I Introduction
- II Méthode de dichotomie
- III Méthode de point fixe
- IV Méthode de Newton
- V Méthode de Lagrange
- VI Bibliographie
- VII Exercices
- Index
Une équation de type f(x) = 0 peut être écrite d'une manière équivalente sous la forme de g(x) = x. La fonction g est une fonction dépendante de f non unique comme le montre l'exemple suivant :
Exemple
Si
la fonction
g peut être
ou
Les instructions Matlab suivantes permettent de tracer les représentations graphiques de ces fonctions, y compris celle de la droite y = x:
Code Matlab
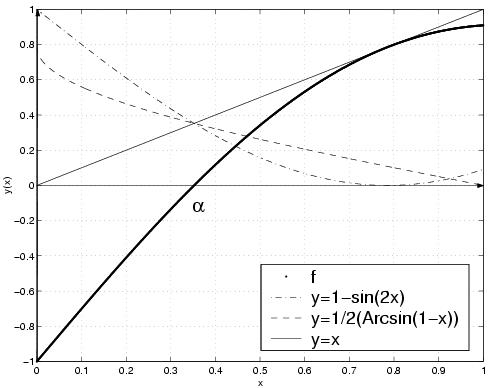
On voit bien que f admet un unique zéro et que les graphes des fonctions
se coupent en
.
Les instructions Matlab suivantes permettent de tracer les représentations graphiques de ces fonctions, y compris celle de la droite y = x:
Code Matlab
x = 0:0.001:1;
f = inline('sin(2*x)-1 + x');
g1 = inline('1-sin(2*x)');
g2 = inline('1/2*(asin(1-x))');
h = inline('x');
plot(x, f(x), '--.b', x, g1(x), '-.b', x, g2(x), '--b', x, h(x),'b');
legend('f', 'y=1-sin(2x)', 'y=1/2*(Arcsin(1-x))', 'y=x');
grid on;
ylabel('y(x)');
xlabel('x');

On voit bien que f admet un unique zéro et que les graphes des fonctions
I-3-1 Point fixe
Résolution numérique de l'équation f ( x ) = 0
→
I Introduction
→
I-3 Rappels d'analyse
→ I-3-1 Point fixe
- I Introduction
- II Méthode de dichotomie
- III Méthode de point fixe
- IV Méthode de Newton
- V Méthode de Lagrange
- VI Bibliographie
- VII Exercices
- Index
Définition
Un réel
est dit point fixe
d'une fonction
si
I-3-2 Multiplicité d'une racine, fonction contractante
Résolution numérique de l'équation f ( x ) = 0
→
I Introduction
→
I-3 Rappels d'analyse
→ I-3-2 Multiplicité d'une racine, fonction contractante
- I Introduction
- II Méthode de dichotomie
- III Méthode de point fixe
- IV Méthode de Newton
- V Méthode de Lagrange
- VI Bibliographie
- VII Exercices
- Index
Définition
Soit
p un entier et
f une fonction
p fois dérivable.
Définition
Remarque
- Soit
. Si
alors g est contractante sur .
- Une fonction contractante est continue.
I-3-3 Théorème de point fixe
Résolution numérique de l'équation f ( x ) = 0
→
I Introduction
→
I-3 Rappels d'analyse
→ I-3-3 Théorème de point fixe
- I Introduction
- II Méthode de dichotomie
- III Méthode de point fixe
- IV Méthode de Newton
- V Méthode de Lagrange
- VI Bibliographie
- VII Exercices
- Index
Théorème
Soit
une fonction contractante de rapport
k. Alors
g admet un unique
point fixe
.
De plus, pour tout choix de
la suite définie par
converge vers
l quand
.
Démonstration
Etape 1: Existence de l et convergence de la suite
Remarquons d'abord que
ce qui implique que la suite
(xn) est
bien définie.
Soit
x0 dans
et
. Nous allons montrer:
Par hypothèse, on sait que
Par récurrence sur
n, on obtient:
Soit
et
on a donc:
La suite
(xn) est donc de Cauchy dans
qui est complet et par
conséquent
(xn) converge vers une limite
l quand
. Comme la fonction
g est contractante, elle est continue, et
donc
quand
. En
passant à la limite dans l'égalité:
on en
déduit que
l = g(l), c'est à dire que
l est un point fixe de
g.
Etape 2: Unicité
Soient l1 et l2 deux points fixes de g, donc alors ; comme k<1, ceci est impossible sauf si l1 = l2.
- est de Cauchy (donc convergente, car est complet)
- quand où l est un point fixe de g.
Par hypothèse, on sait que
Etape 2: Unicité
Soient l1 et l2 deux points fixes de g, donc alors ; comme k<1, ceci est impossible sauf si l1 = l2.
Remarque
Si
g est une application vérifiant
alors la suite définie par
converge vers l'unique point fixe
l de
g sur
pour tout choix de
.
De plus en faisant tendre
p vers l'infini dans
et en gardant
n, on obtient:
I-3-4 Fonctions convexes
Résolution numérique de l'équation f ( x ) = 0
→
I Introduction
→
I-3 Rappels d'analyse
→ I-3-4 Fonctions convexes
I-3-5 Vitesse de convergence d'une suite
Résolution numérique de l'équation f ( x ) = 0
→
I Introduction
→
I-3 Rappels d'analyse
→ I-3-5 Vitesse de convergence d'une suite
- I Introduction
- II Méthode de dichotomie
- III Méthode de point fixe
- IV Méthode de Newton
- V Méthode de Lagrange
- VI Bibliographie
- VII Exercices
- Index
Définition
Soit
une suite convergente vers
 .
On appelle ordre de convergence de la suite
(xn) le réel fini ou infini
r>0 défini par:
.
On appelle ordre de convergence de la suite
(xn) le réel fini ou infini
r>0 défini par:
 .
On appelle ordre de convergence de la suite
(xn) le réel fini ou infini
r>0 défini par:
.
On appelle ordre de convergence de la suite
(xn) le réel fini ou infini
r>0 défini par:
Exemple
Soit
. Soit la suite récurrente
définie par
avec
La suite
(xn) converge vers
et son ordre de
convergence est égal à
2. En effet:
et
I-4 Critère d'arrêt pour la résolution numérique de f(x) = 0
Résolution numérique de l'équation f ( x ) = 0
→
I Introduction
→ I-4 Critère d'arrêt pour la résolution numérique de f(x) = 0
- I Introduction
- II Méthode de dichotomie
- III Méthode de point fixe
- IV Méthode de Newton
- V Méthode de Lagrange
- VI Bibliographie
- VII Exercices
- Index
Une fois construite la suite (xn) convergeant vers l vérifiant g(l) = l, quand peut-on arrêter les itérations de l'algorithme numérique si l'on désire déterminer une valeur approchée de l avec une tolérance
 fixée à l'avance.
Un bon critère d'arrêt est le contrôle de l'incrément :
fixée à l'avance.
Un bon critère d'arrêt est le contrôle de l'incrément :
- On constate la convergence : les résultats numériques se stabilisent.
- On s'arrête à l'itération
n0 si on peut montrer théoriquement que:
Exemple
Soit
f(x) = x3-4x+1. On vérifie que
f
admet
3 racines réelles
et
en posant
Un simple calcul donne les valeurs suivantes:
On constate que les valeurs numériques se stabilisent et on a alors les valeurs approchées de l1, l2 et l3 à environ près.
x0 | -2 | 0 | 2 |
x1 | -2.125 | 0.25 | 1.875 |
x2 | -2.114975450 | 0.254098301 | 1.860978520 |
x3 | -2.114907545 | 0.254101688 | 1.860805877 |
x4 | -2.114907541 | 0.254101688 | 1.860805853 |
x5 | -2.114907541 | 0.254101688 | 1.860805853 |
x6 | |||
x7 | |||
x8 |
On constate que les valeurs numériques se stabilisent et on a alors les valeurs approchées de l1, l2 et l3 à environ près.
II Méthode de dichotomie
Résolution numérique de l'équation f ( x ) = 0
→ II Méthode de dichotomie
II-1 Principe
Résolution numérique de l'équation f ( x ) = 0
→
II Méthode de dichotomie
→ II-1 Principe
- I Introduction
- II Méthode de dichotomie
- III Méthode de point fixe
- IV Méthode de Newton
- V Méthode de Lagrange
- VI Bibliographie
- VII Exercices
- Index
Considérons une fonction
f continue sur un intervalle
.
On suppose que
f admet une et une seule racine
 dans
et que
f(a) f(b) < 0. On note
le milieu de l'intervalle.
dans
et que
f(a) f(b) < 0. On note
le milieu de l'intervalle.
On recommence le processus en prenant l'intervalle au lieu de dans le premier cas, et l'intervalle au lieu de dans le second cas. De cette manière, on construit par récurrence sur n trois suites (an), (bn) et (cn) telles que et telles que pour tout ,
 dans
et que
f(a) f(b) < 0. On note
dans
et que
f(a) f(b) < 0. On note
- Si f(c) = 0, c'est la racine de f et le problème est résolu.
- Si
nous regardons le signe de
f(a) f(c).
- Si f(a) f(c)<0, alors
- Si f(c) f(b)<0, alors
On recommence le processus en prenant l'intervalle au lieu de dans le premier cas, et l'intervalle au lieu de dans le second cas. De cette manière, on construit par récurrence sur n trois suites (an), (bn) et (cn) telles que et telles que pour tout ,
- Si f(cn) f(bn)<0 alors et .
- Si f(cn) f(an)<0 alors et .
II-2 Etude de la convergence
Résolution numérique de l'équation f ( x ) = 0
→
II Méthode de dichotomie
→ II-2 Etude de la convergence
- I Introduction
- II Méthode de dichotomie
- III Méthode de point fixe
- IV Méthode de Newton
- V Méthode de Lagrange
- VI Bibliographie
- VII Exercices
- Index
Théorème
Soit
f une fonction continue sur
vérifiant
f(a) f(b)<0 et soit
l'unique solution de l'équation
f(x) = 0. Si l'algorithme de
dichotomie arrive jusqu'à l'étape
n alors on a l'estimation:
Par conséquent, la suite
(cn) converge vers
 . C'est aussi vrai si
.
. C'est aussi vrai si
.
 . C'est aussi vrai si
.
. C'est aussi vrai si
.
Démonstration
Il suffit de remarquer qu'à chaque itération, on divise
l'intervalle par deux.
II-3 Test d'arrêt
Résolution numérique de l'équation f ( x ) = 0
→
II Méthode de dichotomie
→ II-3 Test d'arrêt
- I Introduction
- II Méthode de dichotomie
- III Méthode de point fixe
- IV Méthode de Newton
- V Méthode de Lagrange
- VI Bibliographie
- VII Exercices
- Index
Pour que la valeur de cn de la suite à la n-ième itération soit une valeur approchée de
 à
près, il suffit que
n vérifie:
à
près, il suffit que
n vérifie:
 .
.
Exemple
On considère la fonction
sur
l'intervalle
. Le code Matlab suivant
trace le graphe de
f.
Code Matlab
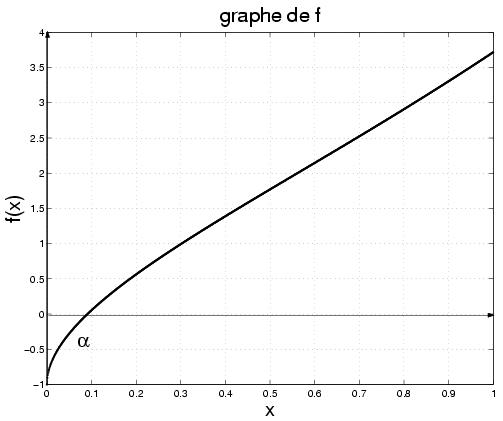
La figure montre que f admet un unique zéro . Si on veut utiliser la méthode de dichotomie pour estimer à une tolérance
près,
il nous faut au plus 33 itérations. En effet, la suite
qui approche
à une tolérance
près,
il nous faut au plus 33 itérations. En effet, la suite
qui approche
 vérifie
et
vérifie
et
Vérification numérique. Le code Matlab suivant permet de calculer la valeur de n nécessaire pour atteindre la précision en choisissant a = 0 et b = 1.
Code Matlab
Résultats
Code Matlab
x = 0:0.001:1;
f = inline('exp(x)+3*sqrt(x)-2');
plot(x, f(x))
grid on;
ylabel('f(x)');
xlabel('x');
title('graphe de f');

La figure montre que f admet un unique zéro . Si on veut utiliser la méthode de dichotomie pour estimer
 à une tolérance
près,
il nous faut au plus 33 itérations. En effet, la suite
qui approche
à une tolérance
près,
il nous faut au plus 33 itérations. En effet, la suite
qui approche
 vérifie
vérifie Vérification numérique. Le code Matlab suivant permet de calculer la valeur de n nécessaire pour atteindre la précision en choisissant a = 0 et b = 1.
Code Matlab
g = inline('exp(t) + 3*sqrt(t)-2');
Nit = 0;
epsilon = 1e-10;
borneinf = 0;
bornesup = 1;
pmilieu = (borneinf + bornesup)/2;
while and(g(pmilieu) ~= 0, (bornesup-borneinf) >= epsilon )
Nit = Nit+1;
if g(pmilieu)*g(borneinf) < 0
bornesup = pmilieu;
else
borneinf = pmilieu;
end
pmilieu = (borneinf + bornesup)/2;
end
pmilieu
g(pmilieu)
Nit - 1
n_theorique = 10*log(10)/log(2) - 1
Résultats
Exemple
Si nous reprenons l'exemple précédent avec la fonction
f(x) = 10x - 5, nous
obtenons les résultats suivants:
On voit alors qu'on atteint la racine sans aucune itération,
ce qui montre contrairement
à l'exemple précédent que la majoration du théorème ci-dessus
est parfois assez large.
sans aucune itération,
ce qui montre contrairement
à l'exemple précédent que la majoration du théorème ci-dessus
est parfois assez large.
On voit alors qu'on atteint la racine
 sans aucune itération,
ce qui montre contrairement
à l'exemple précédent que la majoration du théorème ci-dessus
est parfois assez large.
sans aucune itération,
ce qui montre contrairement
à l'exemple précédent que la majoration du théorème ci-dessus
est parfois assez large.Exercice
Méthode de dichotomie
III Méthode de point fixe
Résolution numérique de l'équation f ( x ) = 0
→ III Méthode de point fixe
III-1 Principe
Résolution numérique de l'équation f ( x ) = 0
→
III Méthode de point fixe
→ III-1 Principe
- I Introduction
- II Méthode de dichotomie
- III Méthode de point fixe
- IV Méthode de Newton
- V Méthode de Lagrange
- VI Bibliographie
- VII Exercices
- Index
Le principe de cette méthode consiste à transformer l'équation f(x) = 0 en une équation équivalente g(x) = x où g est une fonction auxiliaire "bien" choisie. Le point
 est alors un point fixe de
g. Approcher les zéros de
f revient à approcher les points
fixes de
g. Le choix de la fonction
g est motivé par les exigences du
théorème de point fixe. En effet, elle doit être
contractante dans un voisinage
I de
est alors un point fixe de
g. Approcher les zéros de
f revient à approcher les points
fixes de
g. Le choix de la fonction
g est motivé par les exigences du
théorème de point fixe. En effet, elle doit être
contractante dans un voisinage
I de
 , ce qui revient à vérifier
que
sur ce voisinage.
Dans ce cas, on construit une suite
définie par:
, ce qui revient à vérifier
que
sur ce voisinage.
Dans ce cas, on construit une suite
définie par:Il ne reste plus qu'à appliquer localement le théorème de point fixe pour démontrer que
C'est l'objet du paragraphe suivant:
Exercice
Méthode de point fixe
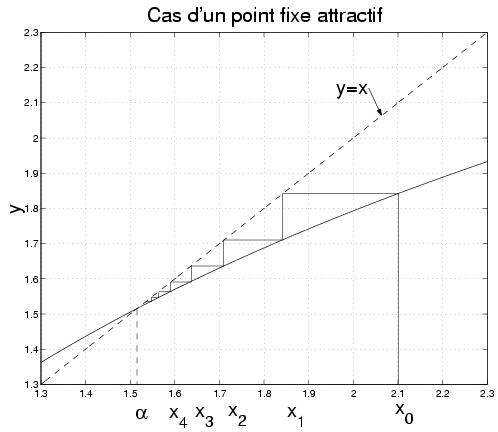
III-2 Point attractif
Résolution numérique de l'équation f ( x ) = 0
→
III Méthode de point fixe
→ III-2 Point attractif
III-2-1 Théorème de convergence
Résolution numérique de l'équation f ( x ) = 0
→
III Méthode de point fixe
→
III-2 Point attractif
→ III-2-1 Théorème de convergence
- I Introduction
- II Méthode de dichotomie
- III Méthode de point fixe
- IV Méthode de Newton
- V Méthode de Lagrange
- VI Bibliographie
- VII Exercices
- Index
Théorème
Soit
de
classe
. On suppose que
g admet un point fixe
vérifiant
. Alors il existe un voisinage
de
 dans
I tel
que la suite
(xn) définie par :
dans
I tel
que la suite
(xn) définie par :
converge vers .
.
 dans
I tel
que la suite
(xn) définie par :
dans
I tel
que la suite
(xn) définie par :converge vers
 .
.Démonstration
Comme
il existe
tel que
. De plus,
g' est continue sur
I donc il existe
un voisinage
tel
que
Donc
g est
k-contractante sur
. En particulier,
.
Le théorème de point fixe appliqué
localement à
g dans le voisinage
implique que
Définition
III-2-2 Illustration graphique
Résolution numérique de l'équation f ( x ) = 0
→
III Méthode de point fixe
→
III-2 Point attractif
→ III-2-2 Illustration graphique
III-2-3 Intervalle de convergence
Résolution numérique de l'équation f ( x ) = 0
→
III Méthode de point fixe
→
III-2 Point attractif
→ III-2-3 Intervalle de convergence
- I Introduction
- II Méthode de dichotomie
- III Méthode de point fixe
- IV Méthode de Newton
- V Méthode de Lagrange
- VI Bibliographie
- VII Exercices
- Index
Proposition
En pratique, un intervalle de convergence
peut être calculé comme suit:
- Si
, prendre comme intervalle de convergence
contenant
 tel que
tel que - Si
, prendre comme intervalle de convergence
tel que
Démonstration
- Cas où
.
D'après la continuité de
g', il existe
contenant
 tel que
On a alorsEn effet, comme g est croissante sur , on a:D'autre part, on aComme ,ce qui donne . Donc . De plus,Comme ,ce qui donne .
tel que
On a alorsEn effet, comme g est croissante sur , on a:D'autre part, on aComme ,ce qui donne . Donc . De plus,Comme ,ce qui donne .
D'où . De plus:-
si
, alors
(xn) est croissante convergeant vers
 ;
;
-
si
, alors
(xn) est décroissante convergeant vers

-
si
, alors
(xn) est croissante convergeant vers
- Cas où
.
D'après la continuité de
g', il existe un voisinage
de
 tel que
et Les réels
tel que
et Les réels et
et
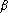 sont nécessairement de part et d'autre de
sont nécessairement de part et d'autre de
 :
ou
.
En effet, on a
Comme , et sont de signes contraires, ce qui prouve le résultat.
:
ou
.
En effet, on a
Comme , et sont de signes contraires, ce qui prouve le résultat.
Montrons que si , alorsOn suppose que ; on a , ce qui implique que , puis queD'où . Soit en supposant que xn et appartiennent à , on montre de la même façon que
On conclut donc que
Remarquons finalement que est toujours entre deux termes successifs
de la suite
(xn). On dit que
(xn) encadre
est toujours entre deux termes successifs
de la suite
(xn). On dit que
(xn) encadre
 .
Par conséquent si
.
.
Par conséquent si
.
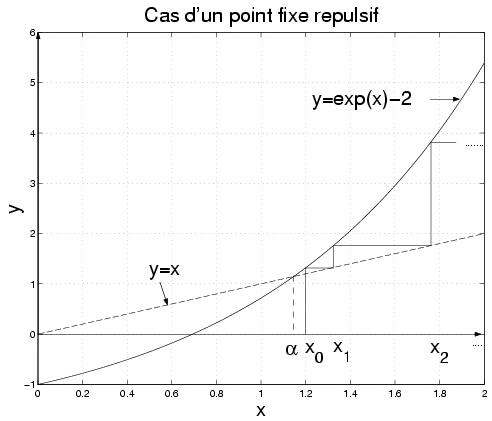
III-3 Point répulsif
Résolution numérique de l'équation f ( x ) = 0
→
III Méthode de point fixe
→ III-3 Point répulsif
III-3-1 Théorème de non-convergence
Résolution numérique de l'équation f ( x ) = 0
→
III Méthode de point fixe
→
III-3 Point répulsif
→ III-3-1 Théorème de non-convergence
III-3-2 Illustration graphique
Résolution numérique de l'équation f ( x ) = 0
→
III Méthode de point fixe
→
III-3 Point répulsif
→ III-3-2 Illustration graphique
III-3-3 Remarque sur la convergence
Résolution numérique de l'équation f ( x ) = 0
→
III Méthode de point fixe
→
III-3 Point répulsif
→ III-3-3 Remarque sur la convergence
III-4 Point douteux
Résolution numérique de l'équation f ( x ) = 0
→
III Méthode de point fixe
→ III-4 Point douteux
III-4-1 Définition
Résolution numérique de l'équation f ( x ) = 0
→
III Méthode de point fixe
→
III-4 Point douteux
→ III-4-1 Définition
III-4-2 Exemple1
Résolution numérique de l'équation f ( x ) = 0
→
III Méthode de point fixe
→
III-4 Point douteux
→ III-4-2 Exemple1
- I Introduction
- II Méthode de dichotomie
- III Méthode de point fixe
- IV Méthode de Newton
- V Méthode de Lagrange
- VI Bibliographie
- VII Exercices
- Index
Exemple
Soit la fonction
g définie par
. On a
et
pour tout
la suite
itérée
(xn) définie par
est
strictement décroissante minorée par
0 donc convergeant vers
une limite
 . Comme
g est continue et que
est l'unique point fixe de
g sur
.
. Comme
g est continue et que
est l'unique point fixe de
g sur
.
 . Comme
g est continue et que
est l'unique point fixe de
g sur
.
. Comme
g est continue et que
est l'unique point fixe de
g sur
.Illustration graphique
Code Matlab
x = -pi/2:0.0001:pi/2;
g = inline('sin(x)');
plot(x, g(x), '--', x, x, '-')
grid on;
ylabel('g(x)');
xlabel('x');
axis on;
title('graphe de g');
III-4-3 Exemple2
Résolution numérique de l'équation f ( x ) = 0
→
III Méthode de point fixe
→
III-4 Point douteux
→ III-4-3 Exemple2
- I Introduction
- II Méthode de dichotomie
- III Méthode de point fixe
- IV Méthode de Newton
- V Méthode de Lagrange
- VI Bibliographie
- VII Exercices
- Index
Exemple
Soit la fonction
.
On a
et pour tout
la suite
itérée
(xn) définie par
est
strictement croissante et non majorée donc divergente. Par conséquent,
le point fixe
de
g est répulsif.
Illustration graphique
Code Matlab
x = -1:0.0001:2;
g = inline('sinh(x)');
plot(x, g(x), '--', x, x, '-')
grid on;
ylabel('g(x)');
xlabel('x');
axis on;
title('graphe de g');

Exercice
Point douteux
III-5 Ordre de convergence
Résolution numérique de l'équation f ( x ) = 0
→
III Méthode de point fixe
→ III-5 Ordre de convergence
- I Introduction
- II Méthode de dichotomie
- III Méthode de point fixe
- IV Méthode de Newton
- V Méthode de Lagrange
- VI Bibliographie
- VII Exercices
- Index
Soit
 un point fixe de
g.
un point fixe de
g.
Nous allons maintenant présenter un résultat simplifié concernant l'ordre de la méthode de point fixe.
Démonstration
 un point fixe de
g.
un point fixe de
g.
Remarque
Si
on sait que
 est un point attractif. Si de plus
g est
de classe
sur
I et s'il existe
M>0 tel que
, pour tout
x dans un voisinage
de
est un point attractif. Si de plus
g est
de classe
sur
I et s'il existe
M>0 tel que
, pour tout
x dans un voisinage
de
 alors
d'après la formule de Taylor :
alors
d'après la formule de Taylor :
d'où
avec
.
La suite
(xn) est alors convergente à convergence au moins quadratique
(voir introduction). est un point attractif. Si de plus
g est
de classe
sur
I et s'il existe
M>0 tel que
, pour tout
x dans un voisinage
de
est un point attractif. Si de plus
g est
de classe
sur
I et s'il existe
M>0 tel que
, pour tout
x dans un voisinage
de
 alors
d'après la formule de Taylor :
alors
d'après la formule de Taylor :
Nous allons maintenant présenter un résultat simplifié concernant l'ordre de la méthode de point fixe.
Théorème
Soit
de
classe
avec
. On suppose que
g admet un unique point fixe
vérifiant
.
Il existe alors un voisinage
de
 dans
I
tel que la suite itérée
(xn) définie par:
converge vers
dans
I
tel que la suite itérée
(xn) définie par:
converge vers
 .
De plus, si
alors l'ordre de convergence de
(xn) est égal à
m.
.
De plus, si
alors l'ordre de convergence de
(xn) est égal à
m.
 dans
I
tel que la suite itérée
(xn) définie par:
dans
I
tel que la suite itérée
(xn) définie par: .
De plus, si
.
De plus, si
Démonstration
L'existence de
de
 est assurée par le théorème de
convergence pour un point attractif. La formule de Taylor appliquée
à la fonction
g au point
est assurée par le théorème de
convergence pour un point attractif. La formule de Taylor appliquée
à la fonction
g au point
 à l'ordre
m donne: il existe un réel
cn dans
l'intervalle
tel que :
Si on suppose de plus que
, alors
Donc,
à l'ordre
m donne: il existe un réel
cn dans
l'intervalle
tel que :
Si on suppose de plus que
, alors
Donc,
 est assurée par le théorème de
convergence pour un point attractif. La formule de Taylor appliquée
à la fonction
g au point
est assurée par le théorème de
convergence pour un point attractif. La formule de Taylor appliquée
à la fonction
g au point
 à l'ordre
m donne: il existe un réel
cn dans
l'intervalle
tel que :
à l'ordre
m donne: il existe un réel
cn dans
l'intervalle
tel que :
- le rapport tend vers qui est fini et non nul,
- pour tout , le rapport tend vers .
III-6 Test d'arrêt
Résolution numérique de l'équation f ( x ) = 0
→
III Méthode de point fixe
→ III-6 Test d'arrêt
- I Introduction
- II Méthode de dichotomie
- III Méthode de point fixe
- IV Méthode de Newton
- V Méthode de Lagrange
- VI Bibliographie
- VII Exercices
- Index
Comme nous l'avons expliqué dans l'introduction, la suite (xn) converge vers un réel
 vérifiant
. En fixant la tolérance
vérifiant
. En fixant la tolérance
 on estime qu'on atteint la précision
on estime qu'on atteint la précision
 dès qu'il existe
tel que:
dès qu'il existe
tel que:Néanmoins, la situation devient plus concrète lorsque g' est négative au voisinage de
 . En effet:
. En effet:Proposition
Soit
de
classe
. On suppose que
g admet un unique point fixe
vérifiant
-1 < g'(x)<0 pour tout
x
dans un intervalle de convergence
de
 . Soit la suite
définie par:
. Soit la suite
définie par:
Alors:
Par conséquent, soit n0 tel que alors approche à
à
 près.
près.
 . Soit la suite
définie par:
. Soit la suite
définie par:Alors:
Par conséquent, soit n0 tel que alors approche
 à
à
 près.
près.Démonstration
On applique le théorème des accroissements finis à
g entre
xn et
 . Il existe alors
cn entre
xn et
. Il existe alors
cn entre
xn et
 telle que:
ce qui donne:
Comme
sont de signes contraires.
telle que:
ce qui donne:
Comme
sont de signes contraires.
 Finalement,
Finalement,
 . Il existe alors
cn entre
xn et
. Il existe alors
cn entre
xn et
 telle que:
telle que:

IV Méthode de Newton
Résolution numérique de l'équation f ( x ) = 0
→ IV Méthode de Newton
IV-1 Principe et convergence
Résolution numérique de l'équation f ( x ) = 0
→
IV Méthode de Newton
→ IV-1 Principe et convergence
- I Introduction
- II Méthode de dichotomie
- III Méthode de point fixe
- IV Méthode de Newton
- V Méthode de Lagrange
- VI Bibliographie
- VII Exercices
- Index
La méthode de Newton est une méthode particulière de point fixe. Elle
est basée sur l'idée de construction d'une suite
(xn) qui
converge vers
 d'une manière quadratique. Rappelons que
d'après le
théorème
, si
g est une application
de
dans
,
on a les résultats suivants:
d'une manière quadratique. Rappelons que
d'après le
théorème
, si
g est une application
de
dans
,
on a les résultats suivants:
Poursuivons maintenant notre construction de la méthode de Newton. Considérons et tel que . Posons
avec
tel que
Nous avons donc
Si on choisit
h pour que
, la méthode de point fixe appliquée
g
donne pour
une suite
(xn) convergeant vers
 d'une manière au moins
quadratique (d'ordre supérieur ou égal à
2). Or
et
donc
Il suffit donc de choisir
h telle que
Ceci n'est
possible que si
d'une manière au moins
quadratique (d'ordre supérieur ou égal à
2). Or
et
donc
Il suffit donc de choisir
h telle que
Ceci n'est
possible que si
En résumé, si est telle que et , on prend pour x assez proche de et la fonction définie par :
vérifie
. Grâce au
théorème
, il existe un voisinage
de
 dans
tel que la suite
(xn) définie
par
est convergente vers
dans
tel que la suite
(xn) définie
par
est convergente vers
 de manière au moins quadratique.
de manière au moins quadratique.
 d'une manière quadratique. Rappelons que
d'après le
théorème
, si
g est une application
de
dans
,
on a les résultats suivants:
d'une manière quadratique. Rappelons que
d'après le
théorème
, si
g est une application
de
dans
,
on a les résultats suivants:
- Si
, et si
alors
et la convergence est linéaire.
- Si
et
, alors
et la convergence est au moins quadratique.
Poursuivons maintenant notre construction de la méthode de Newton. Considérons et tel que . Posons
 d'une manière au moins
quadratique (d'ordre supérieur ou égal à
2). Or
d'une manière au moins
quadratique (d'ordre supérieur ou égal à
2). Or
En résumé, si est telle que et , on prend pour x assez proche de et la fonction définie par :
 dans
tel que la suite
(xn) définie
par
dans
tel que la suite
(xn) définie
par
 de manière au moins quadratique.
de manière au moins quadratique.
Remarque
La suite de Newton vérifie
ou encore
Soit
x0 un point donné (proche de
 ). On considère la droite
D qui passe par le point
et qui a comme pente
f'(xn). Elle a comme équation :
D'après
l'équation
,
est le point où
la droite
D intersecte l'axe
Ox.
). On considère la droite
D qui passe par le point
et qui a comme pente
f'(xn). Elle a comme équation :
D'après
l'équation
,
est le point où
la droite
D intersecte l'axe
Ox.
 ). On considère la droite
D qui passe par le point
et qui a comme pente
f'(xn). Elle a comme équation :
). On considère la droite
D qui passe par le point
et qui a comme pente
f'(xn). Elle a comme équation :
IV-2 Illustration graphique
Résolution numérique de l'équation f ( x ) = 0
→
IV Méthode de Newton
→ IV-2 Illustration graphique
- I Introduction
- II Méthode de dichotomie
- III Méthode de point fixe
- IV Méthode de Newton
- V Méthode de Lagrange
- VI Bibliographie
- VII Exercices
- Index
Code Matlab
x = 0.1:.001:3;
x0 = 2;
x1 = 2*(1 - log(2));
plot(x, x.^-1 - 1 , '-b', x, -(1/x0)^2*(x - x0) + (1/x0 -1), '--b')
grid on;
ylabel('y');
xlabel('x');
title('Illustration de la methode de Newton');
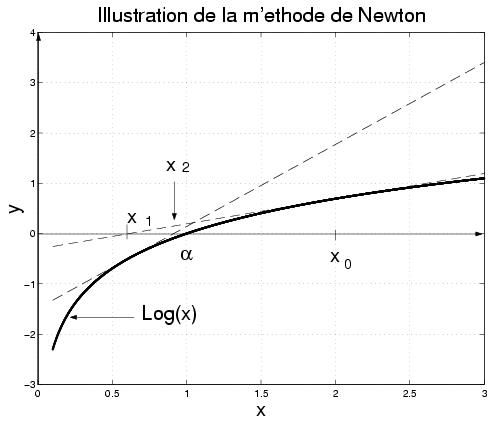
Exercice [ Convergence locale de la méthode de Newton ]
Soit
une fonction de classe
admettant un unique zéro
de multiplicité 1.
- Montrer qu'il existe
tel
que
vérifie
et que la suite
(xn)
définie par :
converge vers
 .
.
- On pose . Montrer que . En déduire que avec
Exercice
Méthode de Newton
Dans ce qui précède, nous avons supposé que la fonction f dont nous cherchons le zéro
 vérifie
vérifie
 est une racine simple de
f. La
question qu'on doit se poser maintenant est : que se passe-t-il quand
est une racine simple de
f. La
question qu'on doit se poser maintenant est : que se passe-t-il quand
 est une racine de
f de multiplicité
? Si on garde
la même fonction
g que précédemment, la méthode de Newton perd son
caractère de convergence quadratique. En effet, on peut écrire
est une racine de
f de multiplicité
? Si on garde
la même fonction
g que précédemment, la méthode de Newton perd son
caractère de convergence quadratique. En effet, on peut écrire
, ce qui implique en terme de suite que tend vers . Ceci se traduit par une convergence linéaire et pas du tout quadratique. Pour récupérer cette dernière, on fait appel à la méthode de Newton modifiée.
IV-3 Méthode de Newton modifiée
Résolution numérique de l'équation f ( x ) = 0
→
IV Méthode de Newton
→ IV-3 Méthode de Newton modifiée
IV-4 Théorème de convergence globale
Résolution numérique de l'équation f ( x ) = 0
→
IV Méthode de Newton
→ IV-4 Théorème de convergence globale
- I Introduction
- II Méthode de dichotomie
- III Méthode de point fixe
- IV Méthode de Newton
- V Méthode de Lagrange
- VI Bibliographie
- VII Exercices
- Index
Nous allons énoncer un résultat de convergence globale ( x0 est choisi n'importe où dans le domaine de f) concernant la méthode de Newton pour des fonctions ayant une concavité déterminée (convexe ou concave).
Théorème
Soit
de classe
vérifiant :
La suite (xn) définie par :
est convergente vers
 .
.
- f(a) f(b)<0
La suite (xn) définie par :
 .
.
Démonstration
Les hypothèses
implique qu'il existe un unique
tel que
.
Comme
est de signe constant, on distingue deux cas :
- Premier cas :
(donc
f(x0)>0).
- Si
on a :
Comme f(x0)>0, alors . Rappelons que g est la fonction définie par . Commeg est croissante sur . D'où, puisque . On en déduit que . De plus,Donc, Par récurrence, on obtient :Donc la suite (xn) est décroissante et minorée par
 , ce qui montre qu'elle est convergente.
Comme
et comme
g est
continue,
(xn) converge vers l'unique point fixe
, ce qui montre qu'elle est convergente.
Comme
et comme
g est
continue,
(xn) converge vers l'unique point fixe
 de
g. On remarque de plus que
de
g. On remarque de plus que
- Si
un raisonnement
semblable au précédent implique que
(xn) est croissante majorée par
 .
Donc
(xn) est convergente. Comme
et que
g est
continue, on obtient que
(xn) converge vers
.
Donc
(xn) est convergente. Comme
et que
g est
continue, on obtient que
(xn) converge vers
 l'unique point fixe
de
g.
l'unique point fixe
de
g.
- Si
on a :
- Second cas :
(donc
f(x0) < 0). Alors le raisonnement précédent,
avec
f remplacée par
-f, implique que
la suite
(xn) converge vers
 .
.
IV-5 Test d'arrêt
Résolution numérique de l'équation f ( x ) = 0
→
IV Méthode de Newton
→ IV-5 Test d'arrêt
- I Introduction
- II Méthode de dichotomie
- III Méthode de point fixe
- IV Méthode de Newton
- V Méthode de Lagrange
- VI Bibliographie
- VII Exercices
- Index
Une fois construite la suite (xn) convergeant vers le réel
 vérifiant
et une fois fixée la tolérance
nous
cherchons le premier entier
n0 vérifiant :
vérifiant
et une fois fixée la tolérance
nous
cherchons le premier entier
n0 vérifiant :
 donné par le théorème des
accroissements finis. Par conséquent,
donné par le théorème des
accroissements finis. Par conséquent,
 fixée.
fixée.
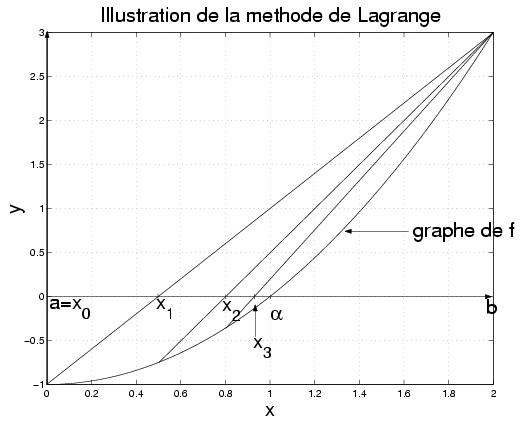
V Méthode de Lagrange
Résolution numérique de l'équation f ( x ) = 0
→ V Méthode de Lagrange
V-1 Principe
Résolution numérique de l'équation f ( x ) = 0
→
V Méthode de Lagrange
→ V-1 Principe
- I Introduction
- II Méthode de dichotomie
- III Méthode de point fixe
- IV Méthode de Newton
- V Méthode de Lagrange
- VI Bibliographie
- VII Exercices
- Index
La méthode de Lagrange est une variante de la méthode
de Newton.
Soit ayant une convexité déterminée. Rappelons que pour calculer un zéro de
f
par la méthode de Newton, on considère la suite
(xn) définie par :
Dans certaines situations, la dérivée de
f est très
compliquée voir même impossible à calculer. Dans ce cas, nous
approchons la dérivée par un taux d'accroissement.
Ce que nous obtenons est appelée la méthode de Lagrange
ou méthode de la sécante :
Ici,
dépend de
xn et de
: on dit que c'est une méthode
à deux pas ; nous avons d'ailleurs besoin de deux itérés initiaux
x0 et
x1.
de
f
par la méthode de Newton, on considère la suite
(xn) définie par :
Dans certaines situations, la dérivée de
f est très
compliquée voir même impossible à calculer. Dans ce cas, nous
approchons la dérivée par un taux d'accroissement.
Ce que nous obtenons est appelée la méthode de Lagrange
ou méthode de la sécante :
Ici,
dépend de
xn et de
: on dit que c'est une méthode
à deux pas ; nous avons d'ailleurs besoin de deux itérés initiaux
x0 et
x1.
L'avantage de cette méthode est qu'elle ne nécessite pas le calcul de la dérivée f'. L'inconvénient est que la convergence n'est plus quadratique.
La fonction g correspondante vérifie :
Soit ayant une convexité déterminée. Rappelons que pour calculer un zéro
 de
f
par la méthode de Newton, on considère la suite
(xn) définie par :
de
f
par la méthode de Newton, on considère la suite
(xn) définie par :
L'avantage de cette méthode est qu'elle ne nécessite pas le calcul de la dérivée f'. L'inconvénient est que la convergence n'est plus quadratique.
La fonction g correspondante vérifie :
V-2 Interprétation géométrique
Résolution numérique de l'équation f ( x ) = 0
→
V Méthode de Lagrange
→ V-2 Interprétation géométrique
V-3 Convergence
Résolution numérique de l'équation f ( x ) = 0
→
V Méthode de Lagrange
→ V-3 Convergence
- I Introduction
- II Méthode de dichotomie
- III Méthode de point fixe
- IV Méthode de Newton
- V Méthode de Lagrange
- VI Bibliographie
- VII Exercices
- Index
Nous allons nous inspirer de l'exemple précédent pour présenter un théorème de convergence.
Théorème
Soit
de classe
telle que
f' et
soient strictement positives sur
. On suppose
que
et on
appelle
 l'unique solution de l'équation
f(x) = 0. Alors
l'unique solution de l'équation
f(x) = 0. Alors
 l'unique solution de l'équation
f(x) = 0. Alors
l'unique solution de l'équation
f(x) = 0. Alors- La suite
(xn) telle que :
est bien définie.
- La suite
(xn) est croissante et converge vers
 .
.
- La méthode de Lagrange est d'ordre au moins 1 :
Démonstration
On pose où
 dans l'intervalle
.
Comme
f(a) < 0 et
f(b) > 0, le réel
x1 est l'abscisse de l'intersection de la
droite passant par
(a, f(a)) et
(b, f(b)) et vérifie
f(x1) < 0 ; de même,
f(x2) < 0 et par récurrence on a
dans l'intervalle
.
Comme
f(a) < 0 et
f(b) > 0, le réel
x1 est l'abscisse de l'intersection de la
droite passant par
(a, f(a)) et
(b, f(b)) et vérifie
f(x1) < 0 ; de même,
f(x2) < 0 et par récurrence on a  ).
).
Exercice
Méthode de Lagrange
VI Bibliographie
Résolution numérique de l'équation f ( x ) = 0
→ VI Bibliographie
- I Introduction
- II Méthode de dichotomie
- III Méthode de point fixe
- IV Méthode de Newton
- V Méthode de Lagrange
- VI Bibliographie
- VII Exercices
- Index
- Philipe G. Ciarlet. Introduction à l'analyse numérique et à l'optimisation . Dunod 1990.
- Jean-Pierre Demailly. Analyse numérique et équations différentielles . Presses Universitaires de Grenoble, 1996.
- Ernst Hairer. Introduction à l'analyse numérique . Université de Genève, section mathématiques, case postale 240. Octobre 2001.
VII Exercices
Résolution numérique de l'équation f ( x ) = 0
→ VII Exercices
- I Introduction
- II Méthode de dichotomie
- III Méthode de point fixe
- IV Méthode de Newton
- V Méthode de Lagrange
- VI Bibliographie
- VII Exercices
- Index
Exercice
On veut calculer les zéros de
l'équation
dans
l'intervalle
. Le graphe de la fonction
f est montré
dans la figure suivante :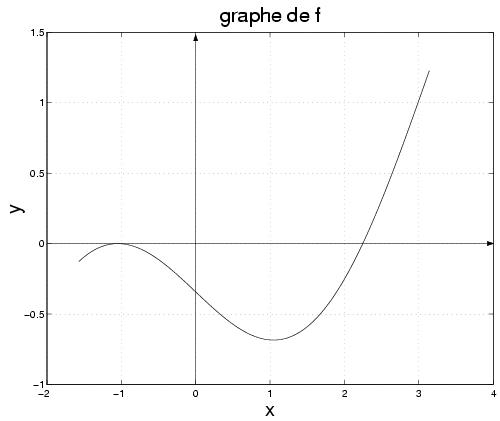

- Peut-on appliquer la méthode de la bissection pour calculer les deux racines ? Pourquoi ? Dans le cas où c'est possible, estimer le nombre minimal d'itérations nécessaires pour calculer le(s) zéro(s) avec une tolérance après avoir choisi un intervalle convenable.
- Ecrire la méthode de Newton pour la fonction f. A l'aide du graphe de la fonction f, déduire l'ordre de convergence de la méthode pour les deux zéros.
- On considère maintenant la méthode de point fixe
avec
pour calculer le zéro . En observant que établir si cette méthode de point fixe est convergente.
- En considérant encore le zéro
et la méthode de point fixe introduite à la
question précédente, montrer qu'il existe une constante positive
C > 0 telle que
et estimer cette constante.
Exercice
On veut calculer le zéro
 de la fonction
f(x) = x3-2 en utilisant la méthode de point fixe
suivante :
étant un paramètre réel.
de la fonction
f(x) = x3-2 en utilisant la méthode de point fixe
suivante :
étant un paramètre réel.
 de la fonction
f(x) = x3-2 en utilisant la méthode de point fixe
suivante :
de la fonction
f(x) = x3-2 en utilisant la méthode de point fixe
suivante :
- Pour quelles valeurs du paramètre w, le zéro de la fonction f est-il un point fixe de la méthode proposée ?
- Pour quelles valeurs de w, la méthode proposée est-elle d'ordre 2 ?
- Existe-t-il une valeur de w telle que l'ordre de la méthode de point fixe est supérieur à 2 ?
Exercice
On considère l'équation non linéaire
sur l'intervalle
.
- Montrer que la fonction
f admet un zéro
 dans
et qu'il est unique.
dans
et qu'il est unique.
- Ecrire la méthode de Newton pour résoudre l'équation f(x) = 0. Quel est l'ordre de convergence de cette méthode ? Justifier la réponse.
- Proposer une méthode d'ordre 2 pour la résolution de l'équation donnée.
Exercice
Soit
 une racine double de la fonction
f :
une racine double de la fonction
f :
 une racine double de la fonction
f :
une racine double de la fonction
f :
- En tenant compte du fait qu'on peut écrire la fonction
f comme
vérifier que la méthode de Newton pour l'approximation de la racine
 est
seulement d'ordre~
1.
est
seulement d'ordre~
1.
- On considère la méthode de Newton modifiée suivante :
Vérifier que cette méthode est d'ordre deux si l'on veut approcher
 .
.
Exercice
On considère la fonction
sur l'intervalle
.
- Montrer qu'il existe un zéro
 pour la fonction
f dans
et
qu'il est unique.
pour la fonction
f dans
et
qu'il est unique.
- On veut calculer le zéro
 de la fonction
f par une méthode de point fixe convenable.
En particulier on se donne deux méthodes de point fixe
où
les fonctions
et
sont définies comme :
Laquelle de ces deux méthodes utiliseriez-vous pour calculer numériquement le zéro
de la fonction
f par une méthode de point fixe convenable.
En particulier on se donne deux méthodes de point fixe
où
les fonctions
et
sont définies comme :
Laquelle de ces deux méthodes utiliseriez-vous pour calculer numériquement le zéro de la
fonction
f ? Justifiez votre réponse.
de la
fonction
f ? Justifiez votre réponse.
- En utilisant la méthode de la bissection sur l'intervalle
estimer le nombre d'itérations nécessaires pour calculer
le zéro
 de la fonction
f avec une tolérance
.
de la fonction
f avec une tolérance
.