et
.
Donner une base
de
qui soit commensurable avec une base de
, ce qui signifie que pour certains entiers
et
positifs,
est une base de
Calculer le plus grand entier
tel que
contienne un sous-groupe isomorphe à
Diviseurs élémentaires et base associée
Le vecteur
Les vecteurs colonnes de la matrice
est le générateur
sont les générateurs
d'un sous-

-module
de
.
Le diviseur élémentaire
Les diviseurs élémentaires
de
, considéré comme sous-module de
,
est
sont, du plus grand au plus petit,
.
Donner une base de
associée à
S'il y a plusieurs diviseurs élémentaires, les séparer par des virgules.
Entrer la base associée en forme d'une matrice où les vecteurs colonnes forment la base associée. Donner d'abord les vecteurs associés aux diviseurs élémentaires dans le même ordre que ceux-là, puis le reste de la base.
Diviseurs élémentaires
Le vecteur
Les vecteurs colonnes de la matrice
est le générateur
sont les générateurs
d'un sous-

-module
de
.
Le diviseur élémentaire
Les diviseurs élémentaires
de
, considéré comme sous-module de
,
est
sont, du plus grand au plus petit,
.
Base d'un réseau
Le dessin ci-dessous montre un réseau dans
, ainsi qu'en couleur rouge un vecteur du réseau qui fait partie d'une base.
Avec lequel des vecteurs en vert le vecteur rouge forme-t-il une base du réseau ? Cliquez sur le point convenable.
Groupes abéliens
Ecrire le groupe abélien
.
.
.
.
sous la forme
,
où
divise
pour tout
.
Groupe d'unités de Z/nZ
Donner les invariants du groupe
dans l'ordre décroissant.
Séparez les invariants par des virgules.
Image d'un Z-module
Trouver deux vecteurs formant une base du

-module engendré par les trois vecteurs :
,
,
.
,
Base d'un sous-Z-module
Trouver une base du

-module engendré par les vecteurs :
j =
Ecrire la réponse sous forme d'une matrice dont les colonnes seront les vecteurs de la base que vous avez trouvée :
Vous pouvez utiliser un logiciel de calcul (sur ce serveur Pari/GP par exemple).
Image d'un Z-module (avec aide)
Trouver deux vecteurs formant une base du

-module engendré par les trois vecteurs :
,
,
.
sachant que
,
Interprétation de la forme de Smith
On veut interpréter l'égalité suivante des matrices
=
sachant que
et
sont de déterminant
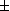
1. On a d'autre part
et
.
Soit
le sous- -module de
engendré par les vecteurs
,
...,
représentés par les colonnes de la matrice
dans la base canonique
,
...,
.
-module de
engendré par les vecteurs
,
...,
représentés par les colonnes de la matrice
dans la base canonique
,
...,
.
Etape 1 : Les vecteurs colonnes de forment
Etape 2 :
Ecrire les vecteurs du nouveau système générateur
,
...,
de
obtenu par cette écriture comme combinaison linéaire des vecteurs
,
...,
(on les écrira dans l'ordre dans lequel ils interviennent naturellement) :
Ecrire ensuite les vecteurs
,
...,
dans la base
,
...,
| w_r = |
+
| e_s |
Donner l'expression de la nouvelle base
,
...,
de
naturellement obtenue par cette écriture dans la base
,
...,
| f_r = |
+
| e_s |
Un multiple de chacun des vecteurs
,
...,
appartient au

-module
. Donner le plus petit multiple (positif) et l'exprimer dans le système générateur des
,
...,
|
f_r = |
+
| v_s |
Consigne : Il n'y a quasiment aucun calcul à faire. Plusieurs réponses sont peut-être possibles, mais la seule acceptée est celle venant directement de l'égalité de matrices données.
Groupes abéliens isomorphes ?
Les deux groupes abéliens suivants sont-ils isomorphes ?
 /
/
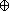
 /
/
et
 /
/
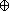
 /
/
Maçonnerie I
([
] en dimension 2) Donner les 6 tailles de briques possibles (avec répétition éventuellement)
,
,
,
,
,
sous la forme 1,2,3
Matrices élémentaires
Si l'on multiplie à une matrice
par la matrice
,
Si l'on multiplie à une matrice
par la matrice
, . Plus précisément,
.
Multiplication/puissance dans Z/nZ
Z-modules et formes normales
Quotient de deux Z-modules
Soit
le sous-

-module de
engendré par
le vecteur
les vecteurs colonnes de la matrice
.
Calculer la décomposition du module quotient
en somme directe d'une partie libre
et de sous-modules de torsion

/

, où
est divisible par
.
= 
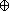
 /
/

Z-modules dans Q^*
Soit l'homomorphisme
de groupes de
dans
défini par
L'image de
est contenue dans le sous-

-module engendré par .
Calculer la matrice de
dans la base canonique de
et dans la base .
La matrice de
dans la base canonique de
et dans la base est
et on a l'égalité

 =
=
Quel est le rang du  -module image de
?
-module image de
?
Quel est le rang du noyau de
?
Donner la base de vecteurs du noyau qui vous est suggérée :
Quel est l'indice de
dans
Relations dans un groupe abélien
Soit
le groupe abélien ayant générateurs dont un système complet de relations est
Donner les invariants du groupe
(il doit y en avoir , d'abord les 0 éventuels, puis les invariants en décroissant y compris les 1 si nécessaire).
Le groupe
est-il fini ?
Les invariants de
sont et
est fini.
n'est pas fini.
- Donner l'exposant de
- Donner l'ordre de
-
est-il cyclique ?
- Donner le rang de
- Donner l'ordre du sous-groupe de torsion maximal de
Relation entière entre des vecteurs
Trouver une combinaison linéaire à coefficients entiers
= 0
entre les trois vecteurs :
,
,
.
On demande une relation génératrice de toutes les combinaisons linéaires entières :
,
,
Surjectivité
L'application linéaire de

-modules
dont la matrice dans les bases canoniques est
est-elle surjective ?
The most recent version
Cette page n'est pas dans son apparence habituelle parce que
WIMS n'a pas pu reconnaître votre navigateur web.
Veuillez noter que les pages WIMS sont générées interactivement; elles ne
sont pas des fichiers
HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE.
Il est inutile pour vous de les ramasser par un programme robot.
- Description: collection d'exercices sur les Z-modules de type fini. interactive exercises, online calculators and plotters, mathematical recreation and games
- Keywords: interactive mathematics, interactive math, server side interactivity, algebra,abstract_algebra, module, abelian_group



 -module engendré par les vecteurs
-module engendré par les vecteurs  -module
de
.
-module
de
.  -module
de
.
-module
de
.  -module engendré par les trois vecteurs :
-module engendré par les trois vecteurs :  -module engendré par les vecteurs :
-module engendré par les vecteurs :  -module engendré par les trois vecteurs :
-module engendré par les trois vecteurs : 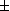 1. On a d'autre part
1. On a d'autre part  -module de
engendré par les vecteurs
,
...,
représentés par les colonnes de la matrice
dans la base canonique
,
...,
.
-module de
engendré par les vecteurs
,
...,
représentés par les colonnes de la matrice
dans la base canonique
,
...,
.  -module
. Donner le plus petit multiple (positif) et l'exprimer dans le système générateur des
,
...,
-module
. Donner le plus petit multiple (positif) et l'exprimer dans le système générateur des
,
...,
 /
/
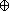
 /
/
 /
/
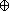
 /
/
 -module de
engendré par
le vecteur
les vecteurs colonnes de la matrice
-module de
engendré par
le vecteur
les vecteurs colonnes de la matrice
 /
/
 , où
est divisible par
.
, où
est divisible par
.
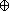
 /
/

 -module engendré par .
-module engendré par . 
 =
=
 -module image de
?
-module image de
? -modules
dont la matrice dans les bases canoniques est
-modules
dont la matrice dans les bases canoniques est