!! used as default html header if there is none in the selected theme. OEF Isométries en dimension 3

OEF Isométries en dimension 3 --- Introduction ---

Ce module regroupe pour l'instant 9 exercices sur les isométries en dimension 3.

Isométrie vectorielle

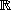Soit un RR-espace vectoriel euclidien de dimension 3 muni d'une base orthonormée directe . On considère l'endomorphisme de de matrice dans =

La matrice est orthogonale car elle vérifie , l'endomorphisme est donc une isométrie.

Est-ce une isométrie ? C'est une rotation. Calculer son angle non orienté (nombre entre 0 et pi ). Cette isométrie une symétrie.

Pour vous aider à faire les calculs :

Isométrie vectorielle (bis)

Soit un -espace vectoriel euclidien de dimension muni d'une base orthonormée directe .

On considère l'endomorphisme de E de matrice dans 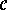calC :

.

La matrice est orthogonale car elle vérifie , donc est une isométrie.

Question 1 : L'isométrie est-elle une symétrie ?

Question 2 : L'isométrie est ou

Question 2 : L'isométrie est ou

Pour vous aider à faire les calculs :

QCM : Isométries affines

Cet exercice a 8 versions différentes. N'hésitez pas à le recommencer.

Dans l'espace affine euclidien de dimension , on considère une isométrie affine d'application linéaire associée .

On suppose que alors peut être

QCM : Points fixes, parties stables

Cet exercice a 9 versions différentes. N'hésitez pas à le recommencer.

Dans l'espace affine euclidien de dimension , on considère une isométrie affine d'application linéaire associée .

On suppose que alors peut être

QCM : Trace d'une isométrie

Dans l'espace affine euclidien de dimension , on considère une isométrie affine d'application linéaire associée .

On suppose que ; alors peut être

Rotation vectorielle

Soit un -espace vectoriel euclidien de dimension muni d'une base orthonormée directe .

On considère la rotation de E de matrice dans

Donnez un vecteur directeur de son axe :

On oriente l'axe de par ce vecteur directeur. Entrez la mesure (sous forme décimale ou en radian) comprise entre - et de l'angle de

Pour vous aider à faire les calculs :

Isométrie avec paramètres

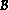Soit calB une base orthonormée directe de l'espace vectoriel euclidien . On pose :

.

Calculer , , et de manière à ce que soit la matrice dans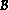 calB d'une .

Pour vous aider à faire les calculs :

Rotation, antirotation

Soit un -espace vectoriel euclidien de dimension muni d'une base orthonormée directe .

On considère l'endomorphisme de E de matrice dans .

La matrice est orthogonale car elle vérifie , donc est une isométrie.

Question 1 : La matrice n'est pas symétrique donc l'isométrie est une ou une

Question 2 : L'isométrie est bien une rotation.

Question 2 : L'isométrie est bien une antirotation. Donnez un vecteur directeur de son axe.

On oriente l'axe de par le vecteur (). Entrez la mesure (sous forme décimale en radian ou comme fraction de pi) comprise entre -pi et pi de l'angle de .

Question 3 : Donnez une équation du plan stable par .

Pour vous aider à faire les calculs :

Réflexion glissée par rapport à un plan

Soit la réflexion par rapport au plan d'équation et la translation de vecteur .
L'isométrie est une . Dans la décomposition canonique de la réflexion glissée L'équation du plan de symétrie l'équation du plan de symétrie est
  • le vecteur de la translation est
    • The most recent version
    Cette page n'est pas dans son apparence habituelle parce que WIMS n'a pas pu reconnaître votre navigateur web.
    Afin de tester le navigateur que vous utilisez, veuillez taper le mot wims ici : puis appuyez sur ``Entrer''.

    Veuillez noter que les pages WIMS sont générées interactivement; elles ne sont pas des fichiers HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE. Il est inutile pour vous de les ramasser par un programme robot.