Géométrie du plan : Frises et Pavages

Géométrie du plan : Frises et Pavages


La première partie de ce document est conçue comme une initiation à la géométrie du plan et une introduction à l'utilisation des groupes. Ce travail mène naturellement à l'étude des frises (ou ornement linéaires) et des pavages, ce que nous faisons ici.
Il a été développé au fil d'un cours d'ouverture à l'intention d'étudiants de L1 et L2 comme une promenade dans la géométrie du plan. Il doit beaucoup à des documents que m'a donnés Daniel Perrin lors de la préparation de ce cours.
frieze pavage

Le plan affine est noté P.

I Frises

II Réseaux et pavages

III D'autres groupes de symétrie

I Frises

Géométrie du plan : Frises et Pavages → I Frises
lambrequin

I-1 Ornement linéaire


Pour analyser une frise, il faut
  • déterminer la bande, c'est-à-dire la direction des translations et un motif de translation ;
  • trouver son groupe ponctuel, les directions des axes de réflexion, l'ordre des rotations ;
  • placer les éléments de symétrie (centres de rotation, axes de réflexion, axes de réflexion glissée).
  • déterminer le groupe de ses isométries parmi une liste finie que nous allons donner.
  • déterminer un motif de base.

Faisons d'abord l'étude mathématique.

I-2 Groupe discret, groupe ponctuel

I-3 Droite affine invariante de la bande

I-4 Classification

I-5 Nomenclature

I-1 Ornement linéaire

Géométrie du plan : Frises et Pavages → I Frises → I-1 Ornement linéaire
Prenons une bande B, c'est-à-dire la zone du plan comprise entre deux droites parallèles et un dessin dans cette bande, c'est-à-dire un sous-ensemble de la bande ou un dessin coloré (un nombre fini de sous-ensembles disjoints de cette bande) contenu dans un parallélogramme et translatons-le dans la direction de la bande de manière à ce qu'il n'y ait pas de superposition, on obtient une frise.

Définition

Un ornement linéaire ou frise est un dessin F de P dont le groupe des translations T(F) de Is(F) est de la forme où est un vecteur non nul.

Définition

Un motif de translation M est une partie fermée de F, connexe (c'est-à-dire d'un seul morceau) telle que les translatés de M par les translations de Is(F) recouvrent F :
et telle que l'intersection de deux tels translatés soit contenue dans leur frontière. Un motif de base M est une partie fermée de F, connexe, telle que les images de M par les isométries de Is(F) recouvrent F :
et telle que l'intersection de deux tels transformés soit contenue dans leur frontière.
Par exemple, un parallélogramme de longueur (dans la direction de la bande) la norme de est un motif de translation. Par contre, le motif de base dépend de la structure du groupe des isométries.

I-2 Groupe discret, groupe ponctuel

Géométrie du plan : Frises et Pavages → I Frises → I-2 Groupe discret, groupe ponctuel

Définition

Un groupe de symétrie d'un ensemble Is(F) est discret s'il existe des réels strictement positifs m1 et m2 tel que
  1. pour toute translation de vecteur non nul appartenant à Is(F), ;
  2. pour toute rotation d'angle 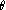theta appartenant à Is(F), .

Proposition

Si Is(F) est discret et laisse fixe un point A, il est fini.

Proposition

Le groupe d'un ornement linéaire est discret.

Proposition

Soit A un point de P. Le groupe ponctuel IsA(F) d'un ornement linéaire est fini.

Désormais, F est un ornement linéaire dont le groupe des translations T(F) de Is(F) est de la forme avec un vecteur non nul. On fixe une origne O du plan.

Proposition

Soit DO la droite vectorielle de direction et la perpendiculaire à DO passant par O. Tout élément de Is(F) est de la forme où t est une translation et
Autrement dit, le groupe ponctuel de Is(F) est contenu dans le groupe .
Démonstration
Soit et écrivons avec gO une isométrie fixant l'origne et un vecteur.
L'isométrie transformée de par g est égale à . Comme appartient à Is(F), aussi ; donc . Comme et ont même norme, est ou .
La droite vectorielle DO de direction est donc stable par gO ; il en est de même de sa perpendiculaire ( gO conserve des angles). Donc, gO peut être : l'identité, la symétrie centrale sO par rapport à O, la réflexion axiale par rapport à DO ou la réflexion axiale par rapport à .

Les sous-groupes de V4 sont faciles à décrire. Il y en a cinq ;
  1. ;
  2. ;
  3. ;
  4. ;
  5. .

Exercice

Quel est le groupe ponctuel de chacune des frises suivantes :
.


.


.


.


.


.


.



Voir aussi Groupe ponctuel d'une frise

I-3 Droite affine invariante de la bande

Géométrie du plan : Frises et Pavages → I Frises → I-3 Droite affine invariante de la bande

Proposition

Il existe au moins une droite affine D parallèle à invariante par Is(F).

Démonstration
Les droites invariantes par le groupe des translations T(F) de Is(F) sont les droites de direction DO. Nous allons donc chercher la droite D parmi ces droites. Elle doit être invariante par les isométries de Is(F) qui ne sont pas des translations.
Prenons une isométrie g de Is(F) qui n'est pas une translation. Elle s'écrit
avec gO = sO, , avec DO de direction et perpendiculaire à DO. Faisons quelques remarques sur les isométries que l'on peut obtenir et les droites qu'elles laissent invariantes :
  •  : g est une symétrie centrale de centre un point A ; toute droite passant par A et de direction DO est invariante par g ;
  • avec D droite de direction DO et parallèle à D (réflexion ou symétrie glissée) ; on a alors . Donc est un multiple de . La droite D est stable par g.
  • avec Delta droite de direction et parallèle à Delta ; on a alors . Donc appartient à T(F) ; comme il est perpendiculaire à , il est nul. Autrement dit, g est une réflexion d'axe Delta perpendiculaire à DO. Toute droite de direction DO est stable par g.

Reprenons maintenant les cinq cas de groupes ponctuels possibles.
  •  : toute droite de direction DO est invariante par Is(F).
  • ; Is(F) est engendré par T et par pour Delta une droite de direction ; toute droite de direction DO est invariante par Is(F).
  • ; toute droite de direction DO est invariante par Is(F).
  • ; il y a dans une réflexion ou une symétrie glissée d'axe une droite D de direction DO. Cette droite est invariante par les translations de Is(F) et par sD donc par Is(F).
  • ; Is(F) est engendré par T et par , et sA avec parallèle à DO, D une droite de direction DO, Delta perpendiculaire à D et A un point. Montrons que la droite D est stable par Is(F) : il reste à montrer que D est stable par sA (pour les autres, on utilise les cas précédents). Pour cela, il suffit de montrer que A appartient à D. L'isométrie suivante appartient à Is(F) :
    avec parallèle à Delta. Son carré est égal à et . Donc et .

I-4 Classification

Géométrie du plan : Frises et Pavages → I Frises → I-4 Classification

Théorème

Il y a exactement 7 groupes de symétrie d'ornements à conjugaison près par une similitude.
On choisit une droite D invariante par Is(F) parallèle à .
  • F1
    .
    Pas grand chose à dire. Le groupe des isométries se réduit au groupe des translations. Il n'y a pas d'axes de symétrie, pas de centre de rotation.
    .
  • F1m
    .
    Une isométrie qui n'est pas une translation est de la forme avec Delta une droite perpendiculaire à D. Les éléments de Is(F) sont de la forme ou , autrement dit avec ou 1. Les axes de symétrie sont distants de . On peut décrire entièrement la loi de groupe par :

    .
  • F1lm
    et il existe une réflexion axiale sD dans Is(F).
    Les éléments du groupe sont de la forme avec et epsilon égal à 0 ou 1. La loi de groupe sur Is(F) est décrite par
    Le groupe est donc commutatif.
    .
  • F1lg
    et il n'existe pas de réflexion axiale dans Is(F).
    Par contre, la réflexion glissée appartient à Is(F). Les éléments de Is(F) sont les et les pour . Le groupe est commutatif.
    .
  • F2
    .
    Les isométries qui ne sont pas des translations sont de la forme , c'est-à-dire des symétries centrales par rapport à un point B. On a . Donc les centres de rotation consécutifs sont à la distance . La loi de groupe est de nouveau donnée par
    avec epsilon et eta égaux à 0 ou à 1.
    .
  • F2mm
    et il existe une réflexion axiale sD dans Is(F). On a aussi dans Is(F) une réflexion axiale et une symétrie centrale de centre A avec A l'intersection de Delta et de D.
    .
  • F2mg
    et il n'existe pas de réflexion axiale d'axe D0 dans Is(F).
    Par contre, il existe une réflexion axiale et une symétrie centrale de centre A. Les axes Delta sont distants de . On a
    avec avec H la projection de A sur Delta.
    .

Exercice

A partir des lettres de l'alphabet, dessiner un ornement de chaque type.

I-5 Nomenclature

Géométrie du plan : Frises et Pavages → I Frises → I-5 Nomenclature
Expliquons les principes de la nomenclature pour les frises (il y a diverses nomenclatures, le tout est d'en choisir une et de la comprendre, elles fonctionnent toutes sur le même principe !) On fait aussi le cas des pavages (le groupe des translations est engendré par deux translations de vecteurs non colinéaires).
On choisit les axes de manière à ce que les axes de symétrie soient perpendiculaires à l'un ou l'autre. Il y a plusieurs caractères. Leur signification est :
  1. une lettre f (en dimension 1) , p, c (en dimension 2) :
    • f quand les translations sont dans une seule direction (groupe de translation isomorphe à );
    • p si les centres de rotation se trouvent sur les axes de symétrie;
    • c si les centres de rotation ne se trouvent pas sur les axes de symétrie.
  2. un entier n indiquant le plus grand ordre de rotation
  3. un symbole indiquant un axe de symétrie perpendiculaire à l'axe des x
    • m pour symétrie miroir,
    • g pour symétrie glissée
    • l pour rien
  4. (cas des pavages) un symbole indiquant un axe de symétrie faisant un angle alpha (différent de l'angle droit) avec l'axe des x.
    • m pour symétrie miroir,
    • g pour symétrie glissée
    • l pour rien

A partir de ces règles, on peut simplifier en supprimant ce qui n'est pas essentiel, c'est-à-dire n'apportera pas de confusion possible ... On enlève par exemple le 1 en deuxième position, le l en dernière position (puisqu'il indique qu'il n'y a rien) ... On remplace aussi de temps en temps le l par un 1 ...à conjugaison près par une similitude} ? Pratiquement, si vous avez deux frises de même groupe dans le plan, quelles similitudes vont intervenir ? Donner un exemple : faire deux dessins de frises ayant le même groupe de symétrie sur votre feuille et indiquer la similitude en question.  

Exercice

Justifier l'expression Il y a exactement. Vérifier qu'en effet on ne peut pas passer de l'un des 7 groupes à un autre par conjugaison par une similitude.
  {comment}

II Réseaux et pavages

Géométrie du plan : Frises et Pavages → II Réseaux et pavages

II-1 Définition d'un pavage


Nous allons étudier ici les pavages réguliers. On parle alors simplement de pavé au lieu de pavé fondamental. Nous reviendrons plus tard sur ce que signifie les classifier.
Dans le paragraphe suivant, nous allons étudier le cas particulier où le pavé fondamental est un parallélogramme, c'est-à-dire nous intéresser d'abord au sous-groupe des translations.

II-2 Réseaux


Passons à un pavage Pav. Soit T le sous-groupe des translations et L le réseau associé. Le groupe du pavage Is(Pav) est contenu dans dans le groupe Is(L) du réseau L.

II-3 Classifions les pavages

II-1 Définition d'un pavage

Géométrie du plan : Frises et Pavages → II Réseaux et pavages → II-1 Définition d'un pavage

Définition

Des sous-ensembles de (qu'on appelle alors pavés) réalisent un pavage de P si les conditions suivantes sont vérifiées :
  • Chacun de ces sous-ensembles est un fermé borné (compact) d'intérieur non vide.
  • La réunion de ces sous-ensembles est égale à P.
  • Deux quelconques de ces sous-ensembles ont toujours une intersection vide, ou une intersection contenue dans leur frontière.

Ne pas hésiter à donner aux mots frontière et intérieur leur sens en langage naturel.

Définition

Un pavage est régulier si tous les pavés sont isométriques.
Une autre définition directe possible est la suivante :
Définition
On appelle pavage régulier du plan la donnée d'un compact (appelé pavé fondamental) P de , d'intérieur non vide et d'un sous-groupe G du groupe des isométries de tel que
  2. si est d'intérieur non vide, g(P) = h(P).

Le groupe des isométries du pavage est le groupe des isométries de laissant le pavage inchangé.
On utilisera aussi des pavage colorié : dans ce cas et sans donner de définitions précises et lourdes, les couleurs doivent être transformées par les isométries.

II-2 Réseaux

Géométrie du plan : Frises et Pavages → II Réseaux et pavages → II-2 Réseaux

II-2-1 Définition

II-2-2 Base réduite d'un réseau


Nous allons maintenant étudier les groupes de symétries d'un réseau et voir qu'il n'y a que 5 possibilités.

II-2-3 Condition cristallographique

II-2-4 Les types de réseaux

II-2-5 Que signifie classifier ?

II-2-1 Définition

Géométrie du plan : Frises et Pavages → II Réseaux et pavages → II-2 Réseaux → II-2-1 Définition
Soient deux vecteurs et du plan affine muni du repère affine . Dessinons l'ensemble des points M de tels que
avec n et m entiers relatifs. On appelle ces points des noeuds et leur ensemble un réseau. Les vecteurs du réseau sont les vecteurs . On dit que est une base du réseau.
Le pavé (maille du réseau) formé des points avec x et y compris entre 0 et 1 et le groupe de symétrie formé des translations avec n et m entiers relatifs forment un pavage du plan.

 

Exercice

Dessiner les réseaux suivants et justifier leur nom :
  •  : réseau oblique
  •  : réseau rectangle
  •  : réseau losange
  • : réseau losange
  •  : réseau carré
  •  : réseau hexagonal ou équilatéral

 

II-2-2 Base réduite d'un réseau

Géométrie du plan : Frises et Pavages → II Réseaux et pavages → II-2 Réseaux → II-2-2 Base réduite d'un réseau
Un réseau a de nombreuses bases. On aimerait trouver des bases qui soient le plus orthonormées possibles : norme des vecteurs petite et angle des vecteurs le plus proche possible de .

Proposition

Soit L un réseau. On peut trouver une base de L telle que
  1. .
  2. .
Une telle base est appelée base réduite. En particulier, l'angle des vecteurs et est compris entre 60 degrés et 90 degrés.

Proposition

Soit L un réseau et une base réduite. Alors, est de norme minimale parmi les vecteurs de L et est de norme minimale parmi les vecteurs de L différents de .

Démonstration
Soit une base réduite. Posons
Si est un vecteur de L et ,
  1.  : Si n ou m est nul, cela est clair. Sinon, on développe :
    De plus, on a l'égalité si et seulement si nm = -1, et , autrement dit pour les vecteurs dans le cas où l'angle de et de est de 60 degrés.
  2. si ,  : Si n = 0, cela est clair. Sinon,
    De plus, on a l'égalité si et seulement si m2 = 1, nm = -1 et , autrement dit pour les vecteurs dans le cas où l'angle de et de est de 60 degrés. Sans oublier bien sûr les vecteurs et éventuellement .

Pour construire une base réduite, quelques idées à comprendre d'abord :
Exercice [ Retrancher à un multiple de ]
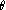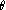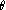Vérifier que si deux vecteurs et font un angle theta compris entre 0 et , alors est de norme plus petite que et l'angle entre et est plus grand que l'angle theta.




 
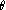Exercice [ Comment choisir ce multiple ]
Comment trouver r entier pour que soit de norme minimale parmi les vecteurs de la forme pour k entier ? Étudier la fonction f définie par . Que peut-on dire alors de l'angle de avec , c'est-à-dire du produit scalaire ?

 

Algorithme

On part des deux vecteurs de base du réseau et on appelle celui qui est de plus petite norme et l'autre. Soit r l'entier le plus proche de . Ainsi, et
  1. Si la norme de est plus petite que celle de , on remplace par et par .
    1. Si le produit scalaire de et de (les nouveaux) est négatif, on remplace par .
    2. On recommence.
  2. Sinon ( ), on choisit ou , de manière à ce que ; alors, est une base réduite car

Proposition

  1. si , les seuls vecteurs de norme sont et ainsi que si l'angle de et de est .
  2. si , les seuls vecteurs de norme sont . Les seuls vecteurs de norme sont .

Démonstration
Supposons et soit . Les vecteurs et conviennent bien sûr. Pour m et n différents de 0, on a
Pour avoir l'égalité, il faut que et que 2x = 1, mn=1. On obtient alors les vecteurs .
Supposons maintenant . On a déjà vu que les seuls vecteurs de norme sont .

II-2-3 Condition cristallographique

Géométrie du plan : Frises et Pavages → II Réseaux et pavages → II-2 Réseaux → II-2-3 Condition cristallographique

Proposition

Soit L un réseau.
  1. Toute rotation du groupe de symétrie d'un réseau est d'ordre 1, 2, 3, 4 ou 6.
  2. Soit H un sous-groupe fini du groupe de symétrie de L. Alors, H est un des groupes Cn, Dn pour n = 1, 2, 3, 4 ou 6.

Ainsi, les ordres possibles de H sont 1, 2, 3, 4, 6, 8 ou 12.
Nous utiliserons dans la démonstration le principe de conjugaison : L'image du centre de rotation d'une rotation d'un groupe de symétrie par une autre rotation du groupe de symétrie est encore un centre de rotation d'un élément du groupe.
Démonstration
Soit G le groupe de symétrie d'un réseau. Soient deux rotations rP et rQ appartenant à G de centre respectivement P et Q et d'ordre . Prenons-les de manière que la distance de P à Q soit minimale [demande un mot d'explication]. Soit n l'ordre de rP. L'isométrie est une rotation de centre R = rP(Q). L'angle est égal à et le triangle est isocèle en P. On a donc . Comme Q R est supérieur ou égal à P Q, on a , donc et .
Donc n est égal à 1, 2, 3, 4, 5 ou 6. Éliminons le cas n = 5.
Supposons qu'il y ait une rotation d'ordre 5 et prenons deux centres P et Q d'ordre 5 à distance minimum. Si on transforme le centre de rotation Q par la rotation de centre P et ses puissances, on obtient cinq points sur le cercle de centre P et de rayon P Q. On recommence en transformant les centres de rotation P par les rotations de centre Q. Un petit calcul (ou un dessin) montre que l'on peut alors trouver deux centres de rotation plus proches que ne le sont P et Q, contradiction.

Remarque
Les cas n = 2, 3, 4, 6 ne peuvent pas être éliminés par cet argument :
n = 2
n = 3
n = 4
n = 5
n = 6
n = 7

II-2-4 Les types de réseaux

Géométrie du plan : Frises et Pavages → II Réseaux et pavages → II-2 Réseaux → II-2-4 Les types de réseaux
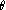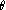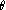Soit ( , ) une base réduite. Notons theta l'angle de et de . Il est compris entre et (entre 60 et 90 degrés).
  • réseau oblique : aucune relation spéciale entre les vecteurs
  • réseau rectangle : et sont perpendiculaires ;
  • réseau losange : et sont de même longueur ;
  • réseau carré : et sont perpendiculaires et de même longueur ;
  • réseau hexagonal ou équilatéral : et sont de même longueur et forment un angle de 60 degrés ;

Dans chacun de ces cas, calculons le groupe des isométries IsO(L) de L laissant fixe l'origine. On note 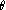theta l'angle des vecteurs et pour une base réduite.

Proposition

Le groupe IsO(L) est déterminé de la manière suivante :
  • réseau oblique, p1
    , theta quelconque. Le groupe IsO(L) est un groupe cyclique d'ordre 2 (type C2 ) :
    (contenu dans ).
    Exemple

  • réseau rectangle, p1mm
    , . Le groupe IsO(L) est le groupe d'un rectangle, il est diédral d'ordre 4 ( D2, mais on le connait aussi sous le nom de groupe de Klein V4) :

    Exemple

  • réseau losange, p6mm
    , theta quelconque. Le groupe de symétrie IsO(L) est le groupe d'un losange, il est diédral d'ordre 4 ( D2 = V4) :

    Exemple

  • réseau carré, p4mm
    , . Le groupe IsO(L) est le groupe d'un carré, c'est un groupe diédral d'ordre 8 ( D4) :

    Exemple
    translate

  • réseau hexagonal ou équilatéral, c1mm
    , . Le groupe IsO(L) est le groupe d'un hexagone, il est diédral d'ordre 12 ( D6) :

    Exemple


Démonstration
Rappelons, que et ont été choisis de manière à ce que et que .
Le groupe IsO(L) ccontient toujours l'identité et la symétrie centrale sO de centre O.
Soit g une isométrie laissant fixe O.
  1. Supposons d'abord que . Les seuls vecteurs de norme sont . Donc, . On pose g0 = g ou , de manière à ce que . Que peut-on dire de ?
    Lorsque est différent de , les seuls vecteurs de norme égale à celle de sont , donc . On a d'autre part .
    1. Si , on a nécessairement . Donc g0 est l'identité et g est soit s0 ou l'identité.
    2. Si , on peut avoir ou . Donc g0 est égale à id ou et g est égale à id, sO, ou à .
    3. Si est égal à , on peut aussi avoir puisque
      et g est alors égale à la réflexion par rapport à la droite vectorielle de direction . Finalement, g peut être égale à id, sO, ou à . Dans ce cas, le parallélogramme construit à l'aide des vecteurs , (qui forment une autre base de L) est un losange. Le parallèlogramme construit à partir de la base réduite n'est ni un rectangle, ni un losange ...
  2. Supposons maintenant que .
    1. Lorsque est différent de , ce qui signifie ici que l'angle de et est différent de 60 degrés ( ), les quatre vecteurs , , , sont de même norme. En utilisant la condition de conservation du produit scalaire, on vérifie qu'on peut obtenir , ou , , c'est-à-dire id, sO, , , , .
    2. Lorsque est égal à , c'est-à-dire lorsque l'angle de et est égal à 60 degrés, les six vecteurs , , , , et sont de même norme que . Si , . On essaye les cinq possibilités restantes pour ; seules sont possibles (déjà trouvée) ou , ce qui donne la rotation d'angle . On fait de même pour et on trouve sans étonnement les rotations d'angle avec k = 0, ..., 5.

II-2-5 Que signifie classifier ?

Géométrie du plan : Frises et Pavages → II Réseaux et pavages → II-2 Réseaux → II-2-5 Que signifie classifier ?
Nous venons de calculer le groupe des isométries laissant fixe un réseau L et l'origine O. On a obtenu quatre groupes possibles non isomorphes : C2, D2, D4 et D6. On a d'autre part obtenu deux fois le groupe D2. Comment peut-on les distinguer ? On a plusieurs manières de dire que deux réseaux sont équivalents mais ces manières ne sont pas équivalentes.
Les notations sont perso ...

Définition

Deux réseaux L1 et L2 sont (lin)-équivalents s'il existe une application linéaire g de P dans P tels que g(L1) = L2.

Pas très intéressant : deux réseaux sont toujours (lin)-équivalents.

Définition

Deux réseaux L1 et L2 sont (sim)-équivalents (semblables) s'il existe une similitude g de P dans P tels que g(L1) = L2.

Très restrictif : en "déplaçant" le réseau dans le plan euclidien (en le translatant, en le faisant tourner, en zoomant, en le reflétant dans un miroir ...), on obtient un réseau équivalent et simplement comme cela.

Définition

Deux réseaux L1 et L2 sont (groupe)-équivalents si leurs groupes d'isométries linéaires IsO(L1) et IsO(L2) sont isomorphes.

Un peu mieux : il y a maintenant quatre types de réseaux à "groupe-équivalence près" correspondant aux groupes C2, D2, D4 et D6.

Définition

Deux réseaux L1 et L2 sont (lin-groupe)-équivalents s'il existe une application linéaire g de P dans P telle que g(L1) = L2 et telle que

Cette définition permet de retrouver les cinq types de réseaux oblique, rectangle, carré, losange et hexagonal. Si vous disposez de deux réseaux de même type, pour montrer qu'ils sont (lin-groupe)-équivalents, on choisit pour g une application linéaire envoyant une base réduite de l'un sur une base réduite de l'autre. Mais il reste quelque chose à montrer : le réseau losange et le réseau rectangle ne sont pas équivalents, c'est-à-dire qu'il n'existe pas d'application linéaire g telle et telle que

Démonstration
Soit s une réflexion de , la droite invariante est de direction un des vecteurs du réseau . Si g existait, alors serait une réflexion par rapport à une droite de direction un des vecteurs du réseau . Mais une telle réflexion n'existe pas dans .

Soit T(L) le groupe des translations de Is(L), c'est-à-dire le groupe des pour .
Les définitions précédentes sont encore valables en remplaçant IsO(L) par Is(L) et donnent le même résultat. Cela vient de la proposition suivante :

Proposition

Soit . Alors, avec et . Autrement dit, le groupe ponctuel de L est égal au sous-groupe de Is(L) formé des isométries laissant fixe O.

Démonstration
Soit et A l'image par g de l'origine O. Ce point A est un point du réseau, donc le vecteur appartient à L. Soit . Comme et g laissent invariant L, il en est de même de g'. De plus , ce qui démontre que .

Cette proposition peut sembler évidente. Cependant, le fait que L est un réseau joue un rôle important. Cela ne serait pas vrai pour n'importe quel ensemble à la place de L.

II-3 Classifions les pavages

Géométrie du plan : Frises et Pavages → II Réseaux et pavages → II-3 Classifions les pavages
Nous allons classifier les pavages selon l'équivalence suivante.

Définition

Deux pavages Pav1 et Pav2 sont équivalents s'il existe une application affine g de P dans P telle que
  1. g(L1) = L2
si les réseaux L1 et L2 sont respectivement les réseaux de Pav1 et de Pav2,

La symétrie de Pav ne peut que diminuer par rapport à celle de L :
On va donc énumérer les différentes possibiités selon le groupe IsO(L).

II-3-1 Le groupe ponctuel est contenu dans celui d'un réseau oblique

II-3-2 Le groupe ponctuel est contenu celui d'un réseau rectangle

II-3-3 Le groupe ponctuel est contenu dans le groupe du losange

II-3-4 Le groupe ponctuel est contenu dans le groupe du carré

II-3-5 Le groupe ponctuel est contenu dans le groupe du réseau hexagonal

II-3-1 Le groupe ponctuel est contenu dans celui d'un réseau oblique

Géométrie du plan : Frises et Pavages → II Réseaux et pavages → II-3 Classifions les pavages → II-3-1 Le groupe ponctuel est contenu dans celui d'un réseau oblique
  • p1
    . Le pavé de translation est un pavé de base. On a donc fait tomber la symétrie par rapport à celle du réseau.
    . . .


    .
  • p2
    Is(P) contient une symétrie centrale sO pour un point O. Prenons ce point pour origine.
    Les éléments de Is(Pav) sont de la forme avec ou 1. Le produit de deux éléments se calcule de la manière suivante

    Invariants de symétrie : les centres de rotation (symétrie) forment un réseau homothétique de T de rapport 1/2.
    Les éléments qui ne sont pas des translations sont des symétries centrales par rapport à un point A de .
    . . .


    .

    Démonstration
    Soient A et B deux points tels que sA et sB appartiennent à G. Alors doit appartenir à T. Comme , on a nécessairement . D'autre part, sO appartient à G.

II-3-2 Le groupe ponctuel est contenu celui d'un réseau rectangle

Géométrie du plan : Frises et Pavages → II Réseaux et pavages → II-3 Classifions les pavages → II-3-2 Le groupe ponctuel est contenu celui d'un réseau rectangle

Prenons un rectangle de côté horizontal u et de côté vertical v. Le groupe est contenu dans le groupe du rectangle .
  • p1m
    et il existe dans Is(Pav) une réflexion axiale d'axe une droite D de direction u.
    Le groupe est un sous-groupe de Is(Pav).
    Les éléments de Is(Pav) sont de la forme avec ou 1.
    Le produit de deux éléments se calcule de la manière suivante

    Les éléments de Is(Pav) qui ne sont pas des translations sont toutes des réflexions d'axes de direction u distants de multiples entiers de .
    . . .


    .
    p1m

    {proof} On a les relations .
    {proof}
  • p1g
    et il n'y a pas de réflexion axiale d'axe porté par dans Is(Pav). Par contre, il y a dans Is(Pav) un élément de la forme pour D une droite parallèle à et a non entier. On a alors
    ce qui implique que 2a est un entier. La droite D est un axe de réflexion glissée.
    Alors, appartient à Is(Pav) pour tout entier n. On a donc une infinité d'axes de glissage parallèles et distants d'un multiple entier de .
    Les éléments de Is(Pav) qui ne sont pas des translations sont des composés d'une symétrie par rapport à des axes de direction , c'est-à-dire d'une "symétrie-translation". Ces axes sont distants de multiples entiers de .
    . . .


    .

Dans les trois cas suivants, le groupe ponctuel est . La discussion va porter sur le fait qu'il y a ou non des symétries dans Is(Pav) et sur la position du centre O par rapport aux axes de symétrie ou de symétrie-translation. En effet, le composé d'une symétrie centrale et d'une translation est encore une symétrie centrale. Les réflexions su ou sv se relèvent soient en des réflexions soit en des symétries glissées.
  • p2mm
    et il existe une réflexion sD dans Is(Pav)
    avec D de direction u et un centre A appartenant à D.
    Le composé est une réflexion d'axe la perpendiculaire D' à D passant par A.
    L'ensemble est un sous-groupe de Is(Pav).
    Le produit de deux éléments se calcule de la manière suivante .
    Is(Pav) contient une infinité de réflexions d'axes de direction u, équidistantes de multiples entiers de . Il existe aussi une infinité de réflexions d'axes parallèles à v et elles sont équidistantes de multiples entiers de . Les centres de symétrie sont à l'intersection de ces axes de direction u et v.
    . . .


    .
  • p2mg
    Il existe dans Is(Pav) des réflexions sD par rapport à une droite D de direction u mais aucun centre de symétrie des symétries centrales sA qui sont dant Is(Pav) ne se trouve sur une de ces droites D.
    Il n'y a pas de symétries par rapport à des droites D de direction v mais seulement des symétries glissées d'axe de glissage D.
    Le composé de sA par sD est une symétrie glissée où H est la projection de A sur D.
    La distance d'un axe de symétrie d'une réflexion ou d'un réflexion glissée à un centre de symétrie est un multiple impair de 1/4.
    . . .


    .
  • p2gg
    Aucune réflexion axiale n'est dans Is(Pav). Ainsi, Is(Pav) ne contient que des glissages d'axe parallèle à u ou à v. Les axes sont distants de multiples entiers de . Les centres de symétrie ne se trouvent pas sur les axes.
    . . .


    .

II-3-3 Le groupe ponctuel est contenu dans le groupe du losange

Géométrie du plan : Frises et Pavages → II Réseaux et pavages → II-3 Classifions les pavages → II-3-3 Le groupe ponctuel est contenu dans le groupe du losange
Le losange est construit à partir de deux vecteurs u et v de norme 1. Le groupe de symétrie du losange est d'ordre 4 formé de l'identité, de la symétrie centrale par rapport au centre du losange et des symétries par rapport aux deux diagonales : . Ce groupe a trois sous-groupes différents de lui-même. Le cas où est d'ordre 1 ou est égal à a déjà été traité.
  • c1m
    . Il y a toujours dans Is(Pav) une réflexion axiale de direction u + v. Les autres éléments de G qui ne sont pas des translations sont des réflexions glissées. On trouve qu'il y a toujours des réflexions d'axe u + v. On a aussi toujours des réflexions glissées d'axe u - v.
    . . .


    .
  • c2mm
    . Le groupe Is(Pav) contient toujours au moins une réflexion axiale de direction u + v et une réflexion axiale de direction u - v et des glissages pour ces directions.
    Les intersections des axes des symétries ainsi que celles des axes de glissages sont centre de symétrie.
    . . .


    .

II-3-4 Le groupe ponctuel est contenu dans le groupe du carré

Géométrie du plan : Frises et Pavages → II Réseaux et pavages → II-3 Classifions les pavages → II-3-4 Le groupe ponctuel est contenu dans le groupe du carré

Il est d'ordre 8. Il est composé de id, , , , su, sv, , (réflexions par rapport aux médianes, ou diagonales).
Il possède trois sous-groupes distingués. Deux d'entre eux sont isomorphes à : et .
Le troisième est cyclique d'ordre 4 : .
Le cas où ne contient pas de rotation d'ordre 4 a été étudié dans le cas du rectangle.
  • p4
    est le sous-groupe contenant les rotations d'angle . Le groupe de symétrie Is(Pav) contient alors une rotation d'ordre 4. Les centres de rotation sont des centres de symétrie. Mais il y en a d'autres.

. . .


.

Dans les deux cas suivants, est le groupe du carré tout entier.
  • p4mm
    et il existe une réflexion axiale dans Is(Pav) dont l'axe passe par un centre de rotation. Le groupe de symétrie Is(Pav) contient alors une rotation d'ordre 4. Il existe d'autre part toujours des réflexions (c'est un cas particulier du losange).
    Les centres de symétrie sont alors les intersections des axes de réflexions, les intersections des axes de glissage, les centres de rotations.
    . . .


    .
  • p4gm
    et l'axe d'aucune réflexion axiale ne passe par un centre de rotation, les centres de rotation sont par contre à l'intersection des axes de glissage.
    . . .


    .

II-3-5 Le groupe ponctuel est contenu dans le groupe du réseau hexagonal

Géométrie du plan : Frises et Pavages → II Réseaux et pavages → II-3 Classifions les pavages → II-3-5 Le groupe ponctuel est contenu dans le groupe du réseau hexagonal

Le réseau équilatéral est construit à partir des vecteurs u et v avec . L'angle entre u et v est donc de . C'est un cas particulier du réseau losange. Si G est le centre de gravité de l'hexagone, Le groupe de symétrie du réseau équilatéral (ou hexagonal) est formé
  • des rotations d'angle , , pi, ,
  • des réflexions par rapport aux diagonales (de direction u + v et u-v)
  • des réflexions par rapport aux médianes (de direction u et u)

  • p3
    est cyclique d'ordre 3. Dans Is(Pav), il y a une rotation d'angle de centre le centre de gravité du triangle équilatéral.
    . . .


    .
  • p6
    est cyclique d'ordre 6. Dans Is(Pav), il y a la rotation d'angle de centre O. .
    . . .


    .
  • p3lm
    est d'ordre 6 et égal à
    Is(Pav) contient des réflexions par rapport à des droites parallèles à u et à v et se coupant en O. Ces deux réflexions engendrent un groupe isomorphe au groupe des permutations d'un ensemble à trois éléments.
    . . .


    .
  • p3ml

    . . .


    .
  • p6mm

    . . .


    .

III D'autres groupes de symétrie

Géométrie du plan : Frises et Pavages → III D'autres groupes de symétrie

On connait des dessins ou des objets qui ont une "symétrie" qui n'est pas relié à la géométrie euclidienne du plan. C'est un autre type de groupes qui intervient alors.
Ce qui suit est inachevé ...

III-1 En spirale

III-2 Plan hyperbolique


Pavage de Penrose

III-1 En spirale

Géométrie du plan : Frises et Pavages → III D'autres groupes de symétrie → III-1 En spirale

Exemple [Spirale]

Plaçons-nous dans le plan complexe où l'on a enlevé l'origine 0. Soit h un nombre complexe non nul. L'application est une bijection. Soit Gh le groupe engendré par h dans ou par Sh dans l'ensemble des applications bijectives de dans lui-même.
Par exemple, si h = 2i, c'est le sous-groupe de formé des nombres complexes

III-2 Plan hyperbolique

Géométrie du plan : Frises et Pavages → III D'autres groupes de symétrie → III-2 Plan hyperbolique
C'est le disque unité dans . Les segments sont les arcs de cercles ou de droite orthogonaux au bord (Poincaré, 1880). On part d'un polygone hyperbolique convexe P0 dont les angles sont de la forme où di est un entier supérieur ou égal à 3. On suppose que
  • soit les entiers di sont pairs.
  • soit les côtés de P0 sont égaux.

On construit les polygones symétriques de P0 par rapport à chacun de ses côtés. On obtient ainsi de nouveaux polygones dont on reprend les symétriques par rapport à leurs côtés et ainsi de suite... Tous ces polygones forment un pavage périodique du plan hyperbolique.
Pavage du plan hyperbolique par des polygones

document sur les frises et les pavages conduisant à la notion de groupe.
: tiling,frieze,isometries, group_theory, interactive mathematics, interactive math, server side interactivity

The most recent version
Cette page n'est pas dans son apparence habituelle parce que WIMS n'a pas pu reconnaître votre navigateur web.
Afin de tester le navigateur que vous utilisez, veuillez taper le mot wims ici : puis appuyez sur ``Entrer''.

Veuillez noter que les pages WIMS sont générées interactivement; elles ne sont pas des fichiers HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE. Il est inutile pour vous de les ramasser par un programme robot.