Raisonnements
Sommaire
En mathématiques, lorsqu'on est confronté à une question ou à un problème, le premier travail à faire est de déterminer la nature de ce travail. S'agit-il de:
- Prouver un implication ?
- Prouver une équivalence ?
- Déterminer l'existence d'un objet répondant à des conditions ?
- Démontrer qu'une proposition est vraie pour tout élément a dans un ensemble A, ou pour certains seulement ?
Ce cours est consacré au langage et au raisonnement en mathématiques. Son objectif essentiel est de donner tout son sens à une proposition écrite avec des symboles mathématiques et d'apprendre à les utiliser avec précision (et non comme des abréviations).
Langage mathématique
Dans cette partie, nous définissons une proposition, sa négation, les connecteurs, les quantificateurs et donnons diverses propriétés.
Contenu.- Expressions mathématiques et Exemples d'expressions mathématiques
- Variables libres, variables liées
- Assertions ou Propositions
- Connecteurs : NON, ET et OU
- Implication, équivalence
- Négation d'une assertion utilisant un connecteur et Tables de vérité
- Condition nécessaire, condition suffisante.
- Quantificateurs, première partie
- Quantificateurs, deuxième partie
- Négation d'une assertion utilisant des quantificateurs
- Contraposée et réciproque
Raisonnements
Un raisonnement mathématique est un processus permettant d'établir, à partir de propositions vraies, de nouvelles propositions, de nouveaux résultats en utilisant des principes logiques. Dans cette partie, nous étudions différents types de raisonnement.
Contenu.- Raisonnement par implication
- Raisonnement par équivalence
- Raisonnement par équivalence en deux temps.
- Raisonnement par contraposition
- Raisonnement par l'absurde
- Raisonnement par disjonction des cas
- Méthode par exhaustion
- Raisonnement par analyse-synthèse
- Raisonnement par récurrence
Bibliographie
Langage mathématique
- Expressions mathématiques et Exemples d'expressions mathématiques
- Variables libres, variables liées
- Assertions ou Propositions
- Connecteurs : NON, ET et OU
- Implication, équivalence
- Négation d'une assertion utilisant un connecteur et Tables de vérité
- Condition nécessaire, condition suffisante.
- Quantificateurs, première partie
- Quantificateurs, deuxième partie
- Négation d'une assertion utilisant des quantificateurs
- Contraposée et réciproque
Expressions mathématiques
Le langage mathématique est formé d'expressions mathématiques, qui sont des assemblages de signes qui obéissent à certaines règles.
- les expressions qui servent à désigner des objets mathématiques; nous les appellerons des termes ;
- les expressions qui sont des affirmations de faits concernant des objets mathématiques; nous les appellerons des propositions ou assertions
- ou bien ce sont deux termes et ces deux termes désignent le même objet quelles que soient les circonstances;
- ou bien ce sont deux propositions et ces deux propositions sont en même temps vraies et en même temps fausses, quelles que soient les circonstances.
Dans le cas des propositions, on dit souvent équivalentes au lieu de synonymes.
Des exemples sont à la page suivante.
Exemples d'expressions mathématiques
Considérons les expressions suivantes. Ce sont toutes des expressions mathématiques au sens donné ici , et dans chacune d'elles la variable x désigne un nombre réel.
- x2=1
- x3=1 ou x3= -1
- x=1 ou x= -1
- pour tout réel x, si x2=1 alors x=1 ou x= -1
Les expressions 1 et 4 sont des termes (qui désignent ici des ensembles), les expressions 2, 3 , 5 et 6 sont des propositions.
Les deux termes 1 et 4 sont synonymes car ils désignent exactement le même objet.
Les propositions 2, 3 et 5 sont équivalentes, elles sont vraies exactement
pour les mêmes valeurs (1 et -1) substituées à la variable
x, et fausses pour les autres.
La proposition 6 est une proposition vraie, nous y reviendrons plus loin.
Ces exemples nous montrent que dans la constitution d'expressions mathématiques, termes et propositions peuvent être imbriqués : pour constituer le terme , on a utilisé la proposition x2=1.
Assertions ou Propositions
- Il est jaune n'est pas une assertion : je ne pourrai jamais décider si "il" est jaune ou pas, tant que je ne sais pas de quoi il s'agit.
- Le stylo de Marianne est noir est une assertion (du moins s'il n'y a qu'une seule Marianne et qu'elle n'a qu'un seul stylo).
- x est plus grand que y n'est pas une assertion. Elle est incomplète puisque x et y ne sont pas connus
- Monsieur Martin est un homme brun ou Tous les hommes sont bruns sont des assertions.
- n'est pas une assertion complète. De quels n s'agit-il ?
- Tous les entiers naturels vérifient est une assertion (fausse mais une assertion quand même !)
- n'est pas une assertion. Sa valeur de vérité n'est pas fixe..
- x> 1 n'est pas une assertion, mais soit en est une...
- Tout entier pair supérieur à 3 est la somme de deux nombres premiers. Là, on n'en sait rien encore... Conjecture de Goldbach !!
Cependant, tous les exemples qui précèdent et qui sont pris dans le langage courant peuvent être sujets à caution, comme on le verra dans certains exemples qui suivent.
Ils servent ici à faire le passage avec les mathématiques.
Par ailleurs, en mathématiques, on fait souvent ce qu'on appelle des abus de langage.
Une différence entre le langage courant et les mathématiques est la suivante : tout ce qui n'est pas "vrai" (au sens de la logique) ne doit pas être utilisé dans un raisonnement. Il n'y a donc pas de sous-entendu comme on le fait fréquemment dans la vie courante. Par exemple, l'affirmationLes filles de ce cours sont excellentes ne dit, ni ne prétend rien sur le niveau des garçons, comparativement. Le français peut faire, là, d'autres suppositions !!..
Connecteurs : NON, ET et OU
Les connecteurs permettent de composer de nouvelles assertions. La valeur de vérité de l'assertion obtenue s'exprime, à l'aide d'une table de vérité, en fonction des valeurs de vérité de celles qui la constituent. On définit dans cette page les connecteurs NON, ET et OU.
| NON | ET | OU | ||
|---|---|---|---|---|
| V | V | F | V | V |
| V | F | F | F | V |
| F | V | V | F | V |
| F | F | V | F | F |
Remarques.
- (NON ) est vraie si est fausse, et fausse si est vraie.
- A l'aide d'une table de vérité, on montre : NON (NON ) est équivalente à . Les deux propositions ont la même valeur de vérité.
- La logique classique respecte la règle du tiers exclu : Une assertion est soit vraie, soit fausse.
- L'assertion ET est vraie si et seulement si les deux assertions et sont vraies.
- L'assertion OU est fausse si et seulement si les deux assertions et sont fausses.
- La négation de « » est : « ».
- La proposition «10 est divisible par 3, ou 10 est pair » est vraie car l'une des deux propositions qui la compose est vraie.
- La proposition « x est divisible par 3, et x est pair» n'est vraie que si les deux propositions sont simultanément vraies, c'est-à-dire lorsque x est un multiple de 6.
- La proposition « x est divisible par 3, ou x est pair» n'est fausse que lorsque l'une et l'autre des deux propositions sont fausses, c'est-à-dire lorsque x est un nombre impair non multiple de 3.
Déterminer la table de vérité d'une proposition.
- Deux propositions avec NON, ET, OU
- Trois propositions avec ET, OU
Reconnaître la table de vérité d'une proposition.
- Deux propositions avec NON, ET, OU
- Trois propositions avec ET, OU
Implication, équivalence
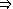
|
||
|---|---|---|
| V | V | V |
| V | F | F |
| F | V | V |
| F | F | V |
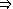 est vraie...
est vraie...
Preuve. Il suffit de comparer les tables de vérité des deux assertions.
L'assertion " est équivalent à " est vraie si et seulement si les deux assertions sont soit simultanément vraies, soit simultanément fausses.
Déterminer la table de vérité d'une proposition.
- Implication et négation de propositions
- Trois propositions avec implication, ET, OU
Reconnaître la table de vérité d'une proposition.
- Implication et négation de propositions
- Trois propositions avec implication, ET, OU
Négation d'une assertion utilisant un connecteur
- La négation de l'assertion ET ] est l'assertion : [(NON ) OU (NON )]
- La négation de l'assertion OU ] est l'assertion : [(NON ) ET (NON )]
- La négation de l'assertion ] est l'assertion : ET (NON )] .
Ces propriétés se démontrent à l'aide de tables de vérité.
Exemple 1. Dans la table ci-dessous, on lit, dans les trois colonnes de gauche, les valeurs de , et [ ET ] et, dans les trois de droite, celles de [NON ], [NON ] et [NON OU NON ]. En considérant les deux colonnes du milieu, on constate que [NON OU NON ] est bien la négation de [ ET ].
| et | NON OU NON | NON | NON | ||
|---|---|---|---|---|---|
| V | V | V | F | F | F |
| V | F | F | V | F | V |
| F | V | F | V | V | F |
| F | F | F | V | V | V |
On en déduit facilement que la négation de [ OU ] est [NON ET NON ].
Exemple 2. Dans la table ci-dessous, on démontre que [ ET NON ] est la négation de [ ] qui est définie comme [NON OU ].
| NON | NON | ET NON | |||
|---|---|---|---|---|---|
| V | V | F | F | V | F |
| V | F | F | V | F | V |
| F | V | V | F | V | F |
| F | F | V | V | V | F |
On notera que la négation d'une implication n'est pas une implication !
- La négation de l'assertion ET est l'assertion OU .
- La négation de l'assertion (
n est pair)
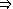 (
n est divisible par
4) est l'assertion (
n est pair) ET (
n n'est pas divisible par
4).
(
n est divisible par
4) est l'assertion (
n est pair) ET (
n n'est pas divisible par
4).
Condition nécessaire, condition suffisante.
- Si
, on dit que
- est une condition suffisante de
- est une condition nécessaire de
- Si , on dit que est une condition nécessaire et suffisante de (et réciproquement).
Remarque: Les cinq énoncés suivants ont la même signification.
- Pour que soit vraie, il faut que soit vraie.
- Pour que soit vraie, il suffit que soit vraie.
- est une condition nécessaire pour avoir .
- est une condition suffisante pour avoir .
Négation d'une assertion utilisant des quantificateurs
- La négation de l'assertion ] est l'assertion ].
- La négation de l'assertion ] est l'assertion ].
Exemple 1. La négation de est multiple de 4 » est n'est pas multiple de 4 » .
Exemple 2. La négation de est » .
Exemple 3. Écrire à l'aide de quantificateurs les phrases suivantes (avec des variables prenant leurs valeurs dans l'ensemble G des guichets et dans l'ensemble J des jours)
: tous les guichets sont fermés certains jours.
: certains jours tous les guichets sont fermés.
Puis écrire leur négation en langage courant et avec des quantificateurs.
Solution( ) : Tous les guichets sont fermés certains jours.
, g est fermé le jour j
( ) : Certains jours tous les guichets sont fermés.
g est fermé le jour j
(non ) : Certains guichets sont ouverts tous les jours.
g est ouvert le jour j
(non ) : Tous les jours, un guichet (au moins) est ouvert.
g est ouvert le jour j
Vous pouvez remarquer que c'est plutôt plus simple mathématiquement :
- on remplace par ,
- on remplace par
- et on remplace l'assertion g est fermé par sa négation qui est ici l'assertion g est ouvert
Exercices.
- Le langage courant utilise souvent des quantificateurs. Essayer de les détecter et donner la négation des assertions qui les utilisent dans l'exercice suivant : Négation de propositions dans le langage courant
- Un quantificateur 1
- Un quantificateur 2
- Un quantificateur et un connecteur
- Un quantificateur et une implication
- Négation de proposition avec deux quantificateurs
Contraposée et réciproque
- La contraposée de l'implication est l'implication .
- La réciproque de l'implication est l'implication .
Démonstration. D'une part, est par définition la proposition [NON OU ]. Et d'autre part, [NON NON ] est la proposition : [NON(NON ) OU NON ], c'est à dire : OU NON ]. C'est bien la même chose.
Dans certains cas, la propriété contraposée peut être sensiblement plus facile à démontrer que la propriété elle-même ; c'est le raisonnement par contraposée .
- Considérons la propriété : « si
est divisible par 4, alors il est pair » (Proposition vraie)
- Sa contraposée est : si est impair, alors, il n'est pas divisible par 4. (Proposition aussi vraie que la première)
- Sa réciproque est : si est pair, alors, il est divisible par 4. (Proposition fausse...)
- Donnons un exemple en langage courant : S'il pleut, le sol est mouillé.
- Sa contraposée est : si le sol n'est pas mouillé, il ne pleut pas énoncée plus couramment : Si le sol est sec, il ne pleut pas. Ces deux implications sont vraies et équivalentes.
- La réciproque de la première est
si le sol est mouillé, il pleut.
Et cette implication est fausse, car le sol peut être mouillé par le passage du camion municipal de nettoyage ou bien par de la neige qui a fondu.
- contraposées et réciproques dans le langage courant.
- contraposées et réciproques en mathématiques.
Contraposée et réciproque : pièges de la vie courante
En fait dans la vie courante on confond très souvent (à tort) contraposée et réciproque, en induisant des sous-entendus qui n’existent pas. Par exemple, si l'on vous dit :Si tu es sage ce matin, tu auras du chocolat cet après-midi
[Notons tout de suite, et c'est important, que cela ne dit rien de ce qui se passera si l'on n'a pas été sage le matin....]la contraposée est
Si tu n'as pas de chocolat cet après-midi, tu n'as pas été sage ce matin
et la réciproqueSi tu as du chocolat cet après-midi, tu as été sage ce matin.
Enfin, la contraposée de la réciproque est
Si tu n'es pas sage ce matin, tu n'auras pas de chocolat cet après-midi.
Ce qui n'est pas équivalent à la première phrase. Mais c'est en général cette dernière affirmation qui est dans la tête de celui qui prononce la première (en appliquant des principes d'éducation positive !)
Raisonnements
- Raisonnement par implication
- Raisonnement par équivalence
- Raisonnement par équivalence en deux temps.
- Raisonnement par contraposition
- Raisonnement par l'absurde
- Raisonnement par disjonction des cas
- Méthode par exhaustion
- Raisonnement par analyse-synthèse
- Raisonnement par récurrence
Raisonnement par implication
Deux règles fondamentales fondent les raisonnements :
- Cette règle utilise la définition de la vérité d'une implication. On l'emploie souvent sans revenir à cette définition.
- Remarque : Si est fausse, alors quelle que soit la valeur de vérité de , l'implication est toujours vraie et ne fournit donc aucun renseignement sur .
- Dans la pratique, le raisonnement commence donc par : "Supposons que est vraie", et on démontre ensuite que l'est aussi.
L'assertion est : le triangle est rectangle.
La réciproque du théorème de Pythagore nous indique que si dans un triangle: A B2 + A C2 = B C2, alors ce triangle est un triangle rectangle. ( )
Conclusion : l'assertion est vraie : A B C est un triangle rectangle
Considérons une fonction
f définie sur
.
On note
l'assertion :
f est dérivable sur
.
On note
l'assertion :
f est continue sur
.
L'assertion
est le théorème : Toute fonction dérivable sur
est continue sur
.
- Supposons que soit vraie pour une fonction f donnée.
- est vraie (c'est le théorème)
Remarque : Dans la pratique, on est souvent conduit à utiliser plusieurs fois de suite la règle, on a ainsi :
Si
est vraie, si
vraie,
si
est vraie, alors
est vraie
Raisonnement par équivalence
Première méthode pour prouver une équivalence :En s'appuyant sur la définition de l'équivalence de deux propositions , on énonce la règle suivante.
Plus généralement, pour démontrer que , on peut aussi établir ainsi une suite d'équivalence entre la première propriété et la propriété , On aura ainsi :
On utilise souvent cette règle pour :
- La résolution d'une équation, d'une inéquation.
- De façon générale pour la détermination de l'ensemble des éléments vérifiant une propriété.
Remarque : Il convient d'être très prudent dans l'établissement des équivalences successives.
On veut résoudre dans , l'équation : . Pour que cette équation ait un sens, x doit vérifier : et . On verra plus loin, que si cette équation a des solutions, l'une des inégalités est automatiquement vérifiée.
"Solution fausse" : "On élève au carré les deux membres", on obtient l'équation du second degré x2+4x-5=0, que l'on résout, ce qui conduit à deux solutions -5 et 1. Si l'on vérifie dans l'équation, on voit que -5 ne convient pas... Que s'est-il passé ? Réponse : on n'a pas raisonné par équivalence !!
La bonne solution impose de formuler le problème avec l'équivalence suivante, en n'oubliant pas les deux conditions :
Et on résout le système, sans oublier l'inéquation, ce qui conduit alors au résultat correct : L'équation n'a qu'une seule solution qui vaut 1.
Raisonnement par équivalence en deux temps.
Deuxième méthode pour prouver une équivalence :Sens direct : Si z est un nombre complexe, il existe a et b réels tels que z = a +ib. Son conjugué est . Si z est réel, sa partie imaginaire est nulle et donc b=0. Ainsi z = a et . L'égalité est démontrée.
Réciproquement : Si , a +ib= a - ib. On a ainsi 2b=0, puis b=0, et donc z =a qui est donc un nombre réel.
L'équivalence est maintenant démontrée.
Sens direct : En développant l'expression, on trouve 2a b = 0, et donc a=0 ou b=0.
Réciproquement : En remplaçant a et b par 0 dans l'expression, on vérifie que les deux membres valent tous les deux zéro, d'où l'égalité.
L'équivalence est maintenant démontrée.
Raisonnement par contraposition
On a vu, dans le paragraphe précédent Contraposée et réciproque , qu'une implication et sa contraposée sont équivalentes.
En d'autres termes, pour démontrer une implication, on peut le faire soit directement, soit en démontrant sa contraposée. En effet, la propriété contraposée peut être sensiblement plus facile à démontrer que la propriété elle-même, comme le montre le cas suivant.
- Pour démontrer que l'implication portant sur des nombres réels :
et
est vraie, il est équivalent, et beaucoup plus simple, de vérifier que la contraposée :[a=0 ou
est vraie, ce qui est évident.
- Démontrer la proposition :
,
n2 impair
impair.
Pour démontrer cette implication, il est plus simple de démontrer la contraposée : , n pair pair.
Ce qui ne présente aucune difficulté. Si n est pair, il existe tel que n=2p. On obtient n2 = (2p)2=4p2 donc le nombre n2 est pair.
Démontrer la proposition : Soit
Démontrer la proposition : , [ si n2-1 n'est pas divisible par 8, alors n est pair].
Raisonnement par l'absurde
Si est vraie et si est une proposition fausse, alors on peut affirmer que est vraie.
En effet : Si (qui est équivalent à ) est vraie, avec fausse, c'est que est vraie.
De l'équation p2 = 2q2, on déduit que p et q sont pairs:
En effet p2 est pair donc p également (ceci découle du fait que la contraposée : p impair impair est vraie, (voir page précédente où cela a été démontré pour les nombres pairs)).
Si p est pair, il existe tel que p = 2k. L'équation p2 = 2q2 devient 4k2=2q2, soit 2k2=q2. Donc q2 est pair et en reprenant le même chose que ci dessus, q est pair. p et q sont donc tous les deux pairs.
Ce qui est en contradiction avec le choix de p et q qu'on a fait (premiers entre eux). D'où la contradiction, ce qui démontre que est un irrationnel.
Montrer qu'il existe une infinité de nombres premiers.
Un raisonnement par l'absurde pour montrer une implication peut parfois être remplacé par un raisonnement par contraposition. Par exemple,
- on veut démontrer que est vraie,
- on suppose (NON ) ET ,
- on finit par démontrer non et on se dit en contradiction avec .
Mais si ne nous a pas servi, on a en fait démontré : et donc par contraposition.
Raisonnement par disjonction des cas
- Si n est pair, il existe p dans tel que n=2p et qui est un entier naturel.
- Si n est impair, il existe p' dans tel que n=2p'+1 et qui est un entier naturel.
Solution
- Si est rationnel, on a fini. Les nombres a= et b= conviennent.
- Sinon les nombres et sont irrationnels et ab vaut 2.
Exercice 1. Démontrer que pour tout entier naturel n, les nombres entiers n2+3n et n(7n+1) sont pairs.
Exercice 2. Disjonction de cas et table de vérité.
Comparer, à l'aide d'une table de vérité, les assertions
]
et [
ET
].
Méthode par exhaustion
Exemple. Trois frères Alfred, Bernard et Claude ont des crayons de couleur différente bleu, rouge et vert. De plus, les assertions suivantes sont vraies :
- Si le crayon d'Alfred est vert, alors le crayon de Bernard est bleu.
- Si le crayon d'Alfred est bleu, alors le crayon de Bernard est rouge.
- Si le crayon de Bernard n'est pas vert, alors le crayon de Claude est bleu.
- Si le crayon de Claude est rouge, alors le crayon d'Alfred est bleu.
Que peut-on conclure sur la couleur respective des crayons d'Alfred, Bernard et Claude? Y a-t-il plusieurs possibilités ?
Exercice. Un scénario de Lewis Caroll
Considérons le problème suivant sachant que
chacune des assertions
suivantes est vraie :
- Ou le malfaiteur est venu en voiture, ou le témoin s'est trompé ;
- Si le malfaiteur a un complice, alors il est venu en voiture ;
- Le malfaiteur n'avait pas de complice et n'avait pas la clé ou bien le malfaiteur avait un complice et avait la clé ;
- Le malfaiteur avait la clé.
Que peut-on en conclure ? Si on remplace la dernière par le malfaiteur n'avait pas la clé, peut-on conclure ?
Raisonnement par analyse-synthèse
Le raisonnement par analyse-synthèse s'utilise souvent dans la recherche d'un ensemble d'éléments vérifiant une propriété . On l'utilise également lorsqu'on ne fait pas de raisonnement par équivalence, dans le but d'arriver au même résultat.
Le principe est le suivant:
- Dans la partie analyse, on cherche les conditions nécessaires que doivent vérifier les éléments satisfaisant .
- Dans la partie synthèse, on s'assure que les éléments satisfaisant les conditions nécessaires obtenues dans la partie analyse vérifient bien .
Démontrer qu'il existe un unique couple (f,g) de fonctions définies sur à valeur dans vérifiant les conditions :
- f est une fonction paire (Rappel : f est paire si )
- g est une fonction impaire (Rappel : g est impaire si )
Analyse : On suppose qu'un tel couple (f,g) existe. Alors, pour tout , on a :
En résolvant le système , on obtient les (uniques) solutions :
et
Synthèse : Il reste à vérifier que ces solutions vérifient bien les trois conditions imposées: f paire, g impaire et , ce qui ne présente aucune difficulté et que nous laissons à faire au lecteur.
Conclusion : On a ainsi trouvé un couple (f,g), avec f paire et g impaire et vérifiant et ce couple est unique.
Raisonnement par récurrence
- Principe de récurrence
- Raisonnement par récurrence : un exemple
- Récurrence : Exercices
- Une récurrence fausse
- Récurrence double
- Récurrence forte
Principe de récurrence
Raisonnement par récurrence : On souhaite démontrer une assertion , pour tout entier naturel n, ou pour des entiers naturels n supérieurs à un entier naturel n0 .Il faut d'abord bien l'énoncer... Ensuite, on suit la démarche suivante en trois étapes:
- On montre qu'il existe un entier
n0 tel que
soit vraie.
C'est l'initialisation en n0. - On montre ensuite que l'assertion :
est vraie pour
.
L'assertion est dite alors héréditaire pour .
Dans la pratique, on nomme "hypothèse de récurrence" la proposition que l'on suppose vraie pour un entier puis on démontre que est vrai. - On énonce la conclusion : Par récurrence, on montre ainsi que la proposition est vraie pour tout entier .
Soyez particulièrement attentifs à la rédaction d'un tel raisonnement.
Exemple : Montrer que la somme des n premiers entiers vaut :
- Initialisation. S1 somme des nombres de 1 à 1 vaut : . C'est juste.
- Hérédité. Soit tel que . Montrons que : = = .
- Conclusion : la propriété est vérifiée, pour tout .
C'est bien ce que l'on cherchait.
Exercice : Montrer que la somme des carrés des n premiers entiers naturels vaut :
Raisonnement par récurrence : un exemple
Donnons une version imagée du principe de récurence (à propos
récurrence vient de courir en arrière).
Mettons 543 dominos sur une table, verticalement et proches les uns des autres. Je désire montrer que,
si je fais tomber le premier domino sur le second, les 543 dominos tombent.
Propriété : les n premiers dominos sont tombés.
- D'une part est vraie car si je fais tomber moi-même le premier domino sur le second, celui-ci tombe, et les deux premiers sont tombés.
- D'autre part, l'assertion
est vraie.
En effet si le n-ième est tombé, il est tombé sur le (n+1)-ième qui tombe à son tour, alors les n+1 dominos premiers sont donc tombés. - L'initialisation et l'hérédité sont prouvées, et par récurrence on a prouvé la proposition , pour n compris entre 2 et 543.
Dans le détail du principe de récurrence :
Comme
(2) et
) sont vraies,
est vraie.
Comme
(3) ) et [
] sont vraies,
est vraie.
.........................
Comme
(542) et [
] sont vraies,
est vraie et les 543 dominos sont tombés.
Conclusion : "Si je fais tomber le premier domino sur le second, les 543 dominos tombent".
Remarquons que si j'avais fait tomber le premier domino de l'autre côté, l'implication serait toujours vraie, en revanche ne le serait pas... Donc ne serait pas vraie (en tout cas sans autre hypothèse et si votre animal préféré arrive, je ne réponds plus de rien).
Récurrence : Exercices
Exercice 1:
À partir de quel rang les quatre propriétés suivantes sont-elles héréditaires? ?
Peut-on les initialiser, et à partir de quel rang ?
Dans les cas suivants, l'assertion
est-elle héréditaire pour tout entier naturel
n ?
Les propositions
sont-elles vraies ?
La proposition
est-elle vraie pour tout entier naturel
n ?
La proposition
est-elle vraie ?
- : n+1 < n
- :
- : 10n - (-1)n est divisible par 11
- : 10n +1 est divisible par 9
Exercice 2: Montrez l'inégalité: . Que pensez-vous de l'énoncé ? Précisez-le et proposez un énoncé correct. Démontrez-le.
Indication : On s’apercevra que l'initialisation ne peut commencer qu'a partir de n=6, et on prouvera qu'en revanche l'hérédité débute à n=2.Une récurrence fausse
Il arrive que l'on fasse une mauvaise hypothèse de récurrence, que la propriété soit fausse pour le n0 choisi, ou que la preuve de l'hérédité ne soit pas valide pour tout n. Trouvez l'erreur dans cette "démonstration" de l'assertionTous les crayons de couleur d'une même boîte sont de même couleur.
"Pseudo-démonstration".- Si la boîte ne contient qu'un seul crayon, tous les crayons de la boîte sont de même couleur. La propriété est donc initialisée.
- Prenons comme hypothèse de récurrence :
Tous les crayons d'une boîte de k crayons sont de même couleur.
Prenons une boîte de crayons contenant k + 1 crayons. Enlevons le crayon A, par exemple. Par hypothèse de récurrence, les k crayons de couleur qui restent ont la même couleur.
Remettons A et enlevons un autre, B. Par hypothèse de récurrence, les k crayons de couleur qui restent ont la même couleur que A. Et, d'après ce qui précède, ils ont aussi la même couleur que B.
Donc les k + 1 crayons de couleur sont tous de la même couleur. L'hérédité est donc "prouvée" - Conclusion : Tous les crayons de couleur d'une même boîte sont de la même couleur.
Récurrence double
Parfois l'hérédité se démontre non pas uniquement par rapport au rang précédent, mais par rapport aux deux précédents. On parle alors de récurrence double. La démarche doit alors être légèrement modifiée.On souhaite démontrer une assertion pour des entiers naturels n supérieurs à un entier naturel n0.
- Initialisation en n0, on montre que et sont vraies.
- On montre ensuite que
l'assertion : [
et
, est vraie pour
.
L'assertion est alors héréditaire pour . - Conclusion: par le principe de récurrence, on a montré que est vraie, pour tout entier .
et
Montrer que l'inégalité suivante est vraie :
- Les deux inégalités suivantes sont vraies : , et .
- Soit , vérifiant les deux inégalités :
et .
Alors :
- Par le principe de récurrence, le résultat est ainsi démontré, pour tout n dans
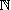
- Montrer par une récurrence double que,
- Question annexe : trouver un réel x, non entier, vérifiant l'hypothèse.
Bibliographie
- F. Liret et D. Martinais, Mathématiques pour le DEUG, Algèbre 1ère Année (Dunod), chapitre 1
- A. Auzimour et F. Petit, Travaux dirigés d'algèbre (Vuibert)
- A. Denmat et F. Héaulme, Algèbre générale (Dunod), td 1