Isométries du plan affine euclidien
Isométries du plan affine euclidien
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Voici un cours sur les isométries du plan avec des figures et des exercices interactifs. L'étude des isométries et des similitudes du plan complexe est l'objet du document Géométrie du plan complexe .
Version en pdf de ce cours avec liens vers les exercices.
Avertissement
Ce cours est une partie de l'option de géométrie enseignée de 2013 à 2015 au premier semestre de la première année de licence MPI à la Faculté des Sciences d'Orsay de l'université Paris Sud. Il s'agissait de pallier l'absence des transformations au Lycée. L'ordre de ce document ne correspond pas à l'ordre du cours.
Merci à Chantal Causse pour les figures illustrant la définition de chaque type d'isométrie.
Merci à Daniel Perrin pour ses suggestions quant à une présentation adaptée des résultats généraux sur les isométries et leur classification.
IV Droites invariantes par des isométries
I Applications du plan affine
Isométries du plan affine euclidien
→ I Applications du plan affine
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Nous commençons avec quelques notions qui posent le cadre de cette étude.
Isométries du plan affine euclidien
→ I Applications du plan affine
I-1 Applications
Isométries du plan affine euclidien
→
I Applications du plan affine
→ I-1 Applications
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Vous connaissez les fonctions à valeurs réelles d'une variable réelle. Elles associent à un nombre réel un autre nombre réel par une formule ou un autre moyen. Certaines sont définies seulement sur une partie de
.
Nous allons étudier des applications du plan affine eucliden .
De plus les applications que nous étudierons seront bijectives :
Nous allons étudier des applications du plan affine eucliden .
Définition
Une application
associe à chaque point
M de
un point
. Chaque point du plan a une et une seule image.
Pour des détails sur la notion d'application consultez le document
Fonctions, applications
.De plus les applications que nous étudierons seront bijectives :
Définition
Par une application bijective, chaque point du plan a un et un seul antécédent. L'inverse
de
est l'application qui à
associe
M. C'est le retour à la position initiale.
Comme au lycée, nous dirons souvent transformation pour une application bijective du plan.
Isométries du plan affine euclidien
→
I Applications du plan affine
→ I-1 Applications
I-1-1 Exemple de la projection
Isométries du plan affine euclidien
→
I Applications du plan affine
→
I-1 Applications
→ I-1-1 Exemple de la projection
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Par contre, la projection orthogonale sur une droite n'est pas bijective et ne conserve pas les distances.
Sur la figure, la droite est l'axe des abscisses. Les longueurs MP et MS sont égales mais M'S' est strictement inférieur à M'P'. On voit aussi que [MP] et [MQ] ont même projeté [M'P'].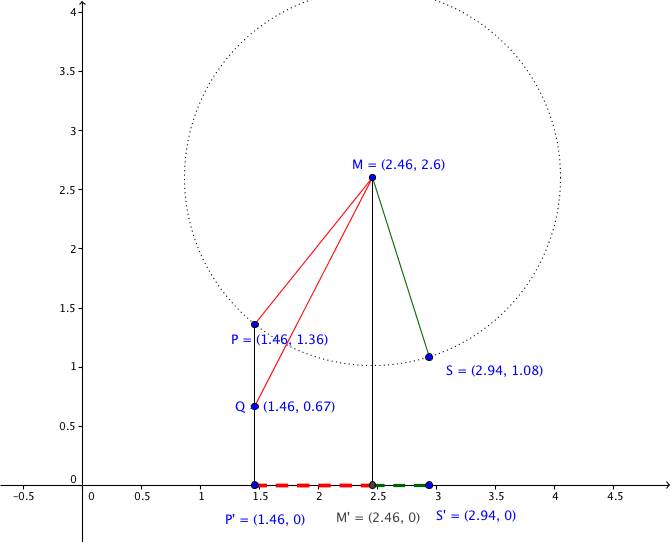
Définition
Dans le plan affine euclidien, on considère une droite
. On appelle projection orthogonale sur
l'application de
dans
qui à
M associe le point
M' intersection de
et de la perpendiculaire à
passant par
M. On dit que
M' est le projeté orthogonal de
M sur
.
Sur la figure, la droite est l'axe des abscisses. Les longueurs MP et MS sont égales mais M'S' est strictement inférieur à M'P'. On voit aussi que [MP] et [MQ] ont même projeté [M'P'].

Isométries du plan affine euclidien
→
I Applications du plan affine
→
I-1 Applications
→ I-1-1 Exemple de la projection
I-1-2 Points fixes
Isométries du plan affine euclidien
→
I Applications du plan affine
→
I-1 Applications
→ I-1-2 Points fixes
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Définition
On dit qu'un point
C est fixe par une application
s'il vérifie
.
Tous les points de l'axe des abscisses sont fixes par la projection de l'exemple précédent.
Isométries du plan affine euclidien
→
I Applications du plan affine
→
I-1 Applications
→ I-1-2 Points fixes
I-2 Isométries
Isométries du plan affine euclidien
→
I Applications du plan affine
→ I-2 Isométries
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Dans ce document, nous nous intéressons aux applications qui conservent les longueurs.
Démonstration
Définition
On dit qu'une application
du plan
dans lui-même est une isométrie si elle conserve les longueurs, c'est-à-dire si l'on a, pour tous points
A et
B dans
,
.
Proposition
Une isométrie transforme trois points alignés en trois points alignés dans le même ordre.
En particulier, une isométrie conserve les milieux.
En particulier, une isométrie conserve les milieux.
Démonstration
On rappelle l'inégalité triangulaire :
Soient
A,
B et
C trois points du plan. On a l'inégalité triangulaire :
L'égalité
A C = A B +B C vaut si et seulement si les trois points sont alignés avec
B entre
A et
C.
Soient trois points
A,
B et
C alignés et
A',
B' et
C' leurs images respectives par une isométrie
. De
A C = A B +B C, on déduit, puisque
est une isométrie,
A'C' = A'B' +B'C'. Donc
A',
B' et
C' sont alignés dans le même ordre que
A,
B et
C.
Le milieu
M de
[A C] est l'unique point vérifiant
A C = A M +M C et
A M=M C. Son image
M' par
vérifie
A'C' = A'M' +M'C' et
A'M' = M'C', c'est donc le milieu de
[A'C'].
Fin de la démonstration
Isométries du plan affine euclidien
→
I Applications du plan affine
→ I-2 Isométries
I-3 Composition, inverse, involution
Isométries du plan affine euclidien
→
I Applications du plan affine
→ I-3 Composition, inverse, involution
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Définition
Si
et
sont deux applications de
dans lui-même, la composée
est l'application de
dans lui-même qui à un point
M associe le point
image de
par
.
On sera attentif au fait qu'on applique d'abord l'application qui est à droite du symbole
de composition.
Remarques
- On note l'application identité du plan. Alors, pour toute application du plan, on a : .
- L'inverse d'une application bijective vérifie .
- On montre facilement que la composée de deux isométries est encore une isométrie.
Définition
On appelle involution une application
, différente de l'identité, qui est son propre inverse pour la loi de composition, c'est-à-dire que
vérifie
.
On dit aussi que
est involutive.
Isométries du plan affine euclidien
→
I Applications du plan affine
→ I-3 Composition, inverse, involution
II Exemples d'isométries
Isométries du plan affine euclidien
→ II Exemples d'isométries
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Les exemples donnés ici recouvrent tous les types d'isométries comme nous le verrons dans la partie
classification
Isométries du plan affine euclidien
→ II Exemples d'isométries
II-1 Translation
Isométries du plan affine euclidien
→
II Exemples d'isométries
→ II-1 Translation
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Au collège, les translations via les parallélogrammes permettaient de définir les vecteurs, ici on suppose donnés les vecteurs. On peut trouver les propriétés caractéristiques du parallélogramme utiles à l'étude des translations dans Droites remarquables, transformations à cette adresse
Parallélogramme
.
Isométries du plan affine euclidien
→
II Exemples d'isométries
→ II-1 Translation
II-1-1 Définition
Isométries du plan affine euclidien
→
II Exemples d'isométries
→
II-1 Translation
→ II-1-1 Définition
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Définition
On appelle translation de vecteur
l'application du plan affine
dans lui-même qui à un point
M associe le point
M' vérifiant
. On la note
.
Sur la figure, le F vert est l'image du F bleu par une translation de vecteur
u. Vous pouvez déplacer tous les objets rouges.
Isométries du plan affine euclidien
→
II Exemples d'isométries
→
II-1 Translation
→ II-1-1 Définition
II-1-2 Propriétés et exercices
Isométries du plan affine euclidien
→
II Exemples d'isométries
→
II-1 Translation
→ II-1-2 Propriétés et exercices
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Proposition
Voici des propriétés d'une translation. D'autres seront établies plus loin.
- Une translation de vecteur non nul n'a pas de points fixes. La translation de vecteur nul est l'identité.
- L'inverse de la translation de vecteur est la translation de vecteur .
- Une translation est une isométrie.
- Soient A et B deux points distincts et A' et B' leurs images respectives par la translation de vecteur . L'image de la droite (A B) par la translation de vecteur est la droite (A'B'). Elle est parallèle à (A B).
- Une translation transforme deux droites parallèles en deux droites parallèles.
Démonstration
1. Un point
M est fixe par la translation de vecteur
si et seulement si on a
, puisque par définition
est égal au vecteur de la translation. Ainsi, seule la translation de vecteur nul admet des points fixes et tout point est fixe par la translation de vecteur nul qui est l'identité.
2. L'inverse de est puisqu'on a, pour tout M du plan, .
3. On pose et , alors on a :
Le quadrilatère
A B B'A' est un parallélogramme donc on a :
. On en déduit :
A'B'=A B, donc
est une isométrie.
4. Comme est une isométrie, l'image de la droite (A B) par la translation est contenue dans la droite (A'B'). De même on a : . L'image de (AB) par est donc la droite (A'B') qui lui est parallèle, en effet les vecteurs directeurs et sont égaux (cf (3)).
5. résulte de 4.
2. L'inverse de est puisqu'on a, pour tout M du plan, .
3. On pose et , alors on a :
4. Comme est une isométrie, l'image de la droite (A B) par la translation est contenue dans la droite (A'B'). De même on a : . L'image de (AB) par est donc la droite (A'B') qui lui est parallèle, en effet les vecteurs directeurs et sont égaux (cf (3)).
5. résulte de 4.
Fin de la démonstration
Remarque
La conservation des angles orientés par une translation est démontrée
ici
et les droites invariantes par une translation sont explicitées
là
.
Exercices
Toutes les propriétés des translations sont utiles pour faire ces exercices. Les trois premiers exercices présentent des données graphiques.
Images de deux points par une translation
Triangles translatés
Cercles translatés
Parallèles et translation
Images de deux points par une translation
Triangles translatés
Cercles translatés
Parallèles et translation
Isométries du plan affine euclidien
→
II Exemples d'isométries
→
II-1 Translation
→ II-1-2 Propriétés et exercices
II-2 Symétrie centrale
Isométries du plan affine euclidien
→
II Exemples d'isométries
→ II-2 Symétrie centrale
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
La symétrie centrale et l'identité sont les seules isométries qui conservent un parallélogramme quelconque.
Isométries du plan affine euclidien
→
II Exemples d'isométries
→ II-2 Symétrie centrale
II-2-1 Définition
Isométries du plan affine euclidien
→
II Exemples d'isométries
→
II-2 Symétrie centrale
→ II-2-1 Définition
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Définition
On appelle symétrie centrale de centre
C l'application du plan affine
dans lui-même qui à un point
M associe le point
M' vérifiant
. On la note
.
Sur la figure, le F vert est l'image du F bleu par la symétrie centrale de centre
C. Vous pouvez déplacer tous les objets rouges.
Isométries du plan affine euclidien
→
II Exemples d'isométries
→
II-2 Symétrie centrale
→ II-2-1 Définition
II-2-2 Propriétés et exercices
Isométries du plan affine euclidien
→
II Exemples d'isométries
→
II-2 Symétrie centrale
→ II-2-2 Propriétés et exercices
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Proposition
Voici des propriétés d'une symétrie centrale. D'autres seront établies plus loin.
- Le centre d'une symétrie centrale est le milieu du segment joignant un point M et son image M'.
- Le centre d'une symétrie centrale est son unique point fixe.
- L'inverse d'une symétrie centrale est elle-même. Une symétrie centrale est donc une involution.
- Une symétrie centrale est une isométrie.
- Soient A et B deux points distincts. L'image de la droite (AB) par une symétrie centrale est la droite passant par les images de A et de B. Elle est parallèle à (AB).
- Une symétrie centrale transforme deux droites parallèles en deux droites parallèles.
Démonstration
Soit
 une symétrie centrale. On note
C son centre :
.
une symétrie centrale. On note
C son centre :
.
1. Par définition, si M est un point et alors : . Le point C est le milieu de [MM'].
2. Le point N est un point fixe si et seulement si il vérifie : si et seulement si le vecteur est nul. Donc C est l'unique point fixe.
3. On a aussi donc M est l'image de par . L'application est son propre inverse. On a .
4. On pose et , alors le quadrilatère ABA'B' est un parallélogramme car ses diagonales se coupent en leur milieu. On a donc : . Par conséquent, est une isométrie : A'B'=AB.
5. Soient et . Les points A, B et M sont alignés, c'est-à-dire que et sont colinéaires. Alors et sont colinéaires donc A', B' et M' sont alignés. L'image de la droite (AB) par est donc contenue dans la droite (A'B'). De même on a : . L'image de (AB) par est donc la droite (A'B') qui lui est parallèle car les vecteurs directeurs et sont égaux.
 une symétrie centrale. On note
C son centre :
.
une symétrie centrale. On note
C son centre :
.
1. Par définition, si M est un point et alors : . Le point C est le milieu de [MM'].
2. Le point N est un point fixe si et seulement si il vérifie : si et seulement si le vecteur est nul. Donc C est l'unique point fixe.
3. On a aussi donc M est l'image de par . L'application est son propre inverse. On a .
4. On pose et , alors le quadrilatère ABA'B' est un parallélogramme car ses diagonales se coupent en leur milieu. On a donc : . Par conséquent, est une isométrie : A'B'=AB.
5. Soient et . Les points A, B et M sont alignés, c'est-à-dire que et sont colinéaires. Alors et sont colinéaires donc A', B' et M' sont alignés. L'image de la droite (AB) par est donc contenue dans la droite (A'B'). De même on a : . L'image de (AB) par est donc la droite (A'B') qui lui est parallèle car les vecteurs directeurs et sont égaux.
Fin de la démonstration
Remarque
La conservation des angles orientés par une symétrie centrale est démontrée
ici
et les droites invariantes par une symétrie centrale sont explicitées
là
.
Exercices
Toutes les propriétés des symétries centrales sont utiles pour faire ces exercices. Les exercices demandent une réponse graphique.
Symétrique d'un point (1)
Symétrique d'un point (2)
Symétrique d'un point (1)
Symétrique d'un point (2)
Isométries du plan affine euclidien
→
II Exemples d'isométries
→
II-2 Symétrie centrale
→ II-2-2 Propriétés et exercices
II-3 Réflexion
Isométries du plan affine euclidien
→
II Exemples d'isométries
→ II-3 Réflexion
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
La réflexion s'appelle "symétrie axiale" au collège.
On peut trouver les propriétés de la médiatrice d'un segment, utiles à l'étude des réflexions dans Droites remarquables, transformations à cette adresse Médiatrice .
On peut trouver les propriétés de la médiatrice d'un segment, utiles à l'étude des réflexions dans Droites remarquables, transformations à cette adresse Médiatrice .
Isométries du plan affine euclidien
→
II Exemples d'isométries
→ II-3 Réflexion
II-3-1 Définition
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Définition
Soit
une droite du plan
. On appelle symétrie orthogonale par rapport à
ou réflexion d'axe
, et on note
, l'application du plan affine
dans lui-même qui à un point
M associe le point
M' tel que
- le milieu de [MM'] appartienne à
- la droite (MM') soit perpendiculaire à .
Sur la figure, l'axe de symétrie est représenté par un trait mixte. L'image du F bleu par la symétrie est le F vert. Vous pouvez déplacer tous les objets rouges.
II-3-2 Propriétés et exercices
Isométries du plan affine euclidien
→
II Exemples d'isométries
→
II-3 Réflexion
→ II-3-2 Propriétés et exercices
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Proposition
Voici des propriétés d'une réflexion. D'autres seront établies plus loin.
- Les points de sont les seuls points fixes.
- L'inverse de est .
- Une réflexion est une isométrie.
- Soient
A et
B deux points distincts et
A' et
B' leurs images respectives par
. L'image par
de
(AB) est
(A'B'). Si deux droites sont parallèles, leurs images sont parallèles.
Démonstration
1. Un point
N est fixe si et seulement si il est confondu avec son image
N' si et seulement si le segment
[NN'] est réduit au point
N qui est aussi son milieu si et seulement si
N appartient à
.
2. La définition d'une réflexion est symétrique en M et M'.
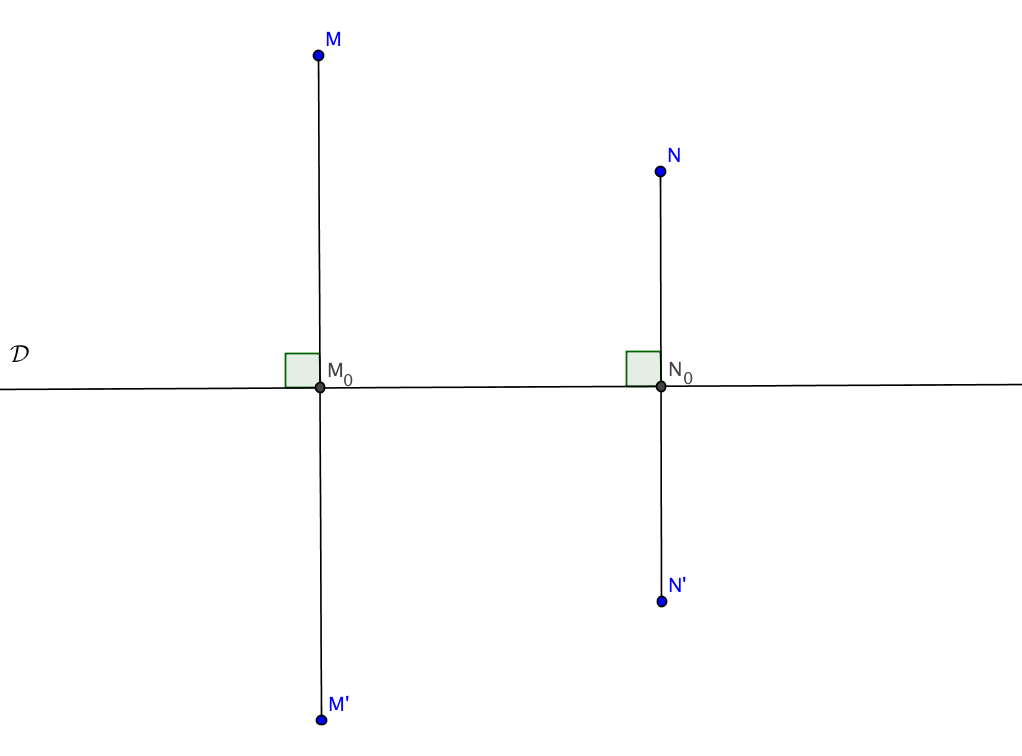
3. Soient M0 et N0 les projetés orthogonaux respectifs de M et N sur , on a :
De même on a :
.
Alors de et on déduit l'égalité M'N'2=MN2. Donc une réflexion est une isométrie.
 4. On a vu qu'une isométrie conserve l'alignement donc l'image de
(AB) par
est contenue dans la droite
(A'B'). Comme
A et
B sont les images de
A' et
B' par
, l'image de
(A'B') par
est contenue dans la droite
(AB), soit
. En appliquant
à cette inclusion, on obtient
. Comme on avait
, on conclut à l'égalité
.
4. On a vu qu'une isométrie conserve l'alignement donc l'image de
(AB) par
est contenue dans la droite
(A'B'). Comme
A et
B sont les images de
A' et
B' par
, l'image de
(A'B') par
est contenue dans la droite
(AB), soit
. En appliquant
à cette inclusion, on obtient
. Comme on avait
, on conclut à l'égalité
.
Soient deux droites parallèles et et et leurs images respectives par . Alors et sont parallèles, en effet si elles étaient sécantes en un point C alors serait commun à et , ce qui est impossible.
2. La définition d'une réflexion est symétrique en M et M'.
3. Soient M0 et N0 les projetés orthogonaux respectifs de M et N sur , on a :
Alors de et on déduit l'égalité M'N'2=MN2. Donc une réflexion est une isométrie.

Soient deux droites parallèles et et et leurs images respectives par . Alors et sont parallèles, en effet si elles étaient sécantes en un point C alors serait commun à et , ce qui est impossible.
Fin de la démonstration
Remarque
Une réflexion transforme un angle orienté en son opposé (voir
ici
). Les droites invariantes par une réflexion sont explicitées
là
.
Exercices
Toutes les propriétés des réflexions sont utiles pour faire ces exercices. Les exercices demandent une réponse graphique.
Symétrique d'un point (1)
Symétrique d'un point (2)
Image d'un triangle par une réflexion (1)
Image d'un triangle par une réflexion (2)
Image d'un triangle par une réflexion (3)
Symétrique d'un point (1)
Symétrique d'un point (2)
Image d'un triangle par une réflexion (1)
Image d'un triangle par une réflexion (2)
Image d'un triangle par une réflexion (3)
Isométries du plan affine euclidien
→
II Exemples d'isométries
→
II-3 Réflexion
→ II-3-2 Propriétés et exercices
II-4 Symétrie glissée
Isométries du plan affine euclidien
→
II Exemples d'isométries
→ II-4 Symétrie glissée
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Quel est le type de la composée d'une translation et d'une réflexion ? Voici la réponse dans un cas particulier, quand l'axe de la réflexion est dirigé par le vecteur de la translation. Nous découvrons un nouveau type d'isométrie sans point fixe qui n'est pas une translation.
Isométries du plan affine euclidien
→
II Exemples d'isométries
→ II-4 Symétrie glissée
II-4-1 Définition
Isométries du plan affine euclidien
→
II Exemples d'isométries
→
II-4 Symétrie glissée
→ II-4-1 Définition
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Définition
On appelle symétrie glissée la composée d'une réflexion et d'une translation de vecteur dirigeant l'axe de la réflexion.
Une symétrie glissée est une isométrie comme composée d'isométries.Sur la figure, l'axe de symétrie est représenté par un trait mixte, et le vecteur est représenté en vert. L'image du F bleu par la symétrie glissée d'axe D et de vecteur u est le F vert. Vous pouvez déplacer tous les objets rouges.
Isométries du plan affine euclidien
→
II Exemples d'isométries
→
II-4 Symétrie glissée
→ II-4-1 Définition
II-4-2 Propriétés et exercice
Isométries du plan affine euclidien
→
II Exemples d'isométries
→
II-4 Symétrie glissée
→ II-4-2 Propriétés et exercice
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Proposition
Soit
 une droite dirigée par un vecteur
. La symétrie glissée
vérifie ces propriétés :
une droite dirigée par un vecteur
. La symétrie glissée
vérifie ces propriétés :
 une droite dirigée par un vecteur
. La symétrie glissée
vérifie ces propriétés :
une droite dirigée par un vecteur
. La symétrie glissée
vérifie ces propriétés :
- Les applications et commutent. On a aussi .
- Le carré
de
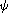 vaut
.
vaut
.
- La décomposition est unique.
- L'application n'admet aucun point fixe.
- La droite
est l'ensemble des milieux de
pour
.
Démonstration
1. Les applications
et
commutent si et seulement si on a l'égalité
. Soit un point
M du plan, on pose
Par l'égalité , le quadrilatère M M1 M2 M3 est un parallélogramme. Comme dirige et que (M1 M2) est perpendiculaire à , l'angle est droit donc M M1 M2 M3 est un rectangle.
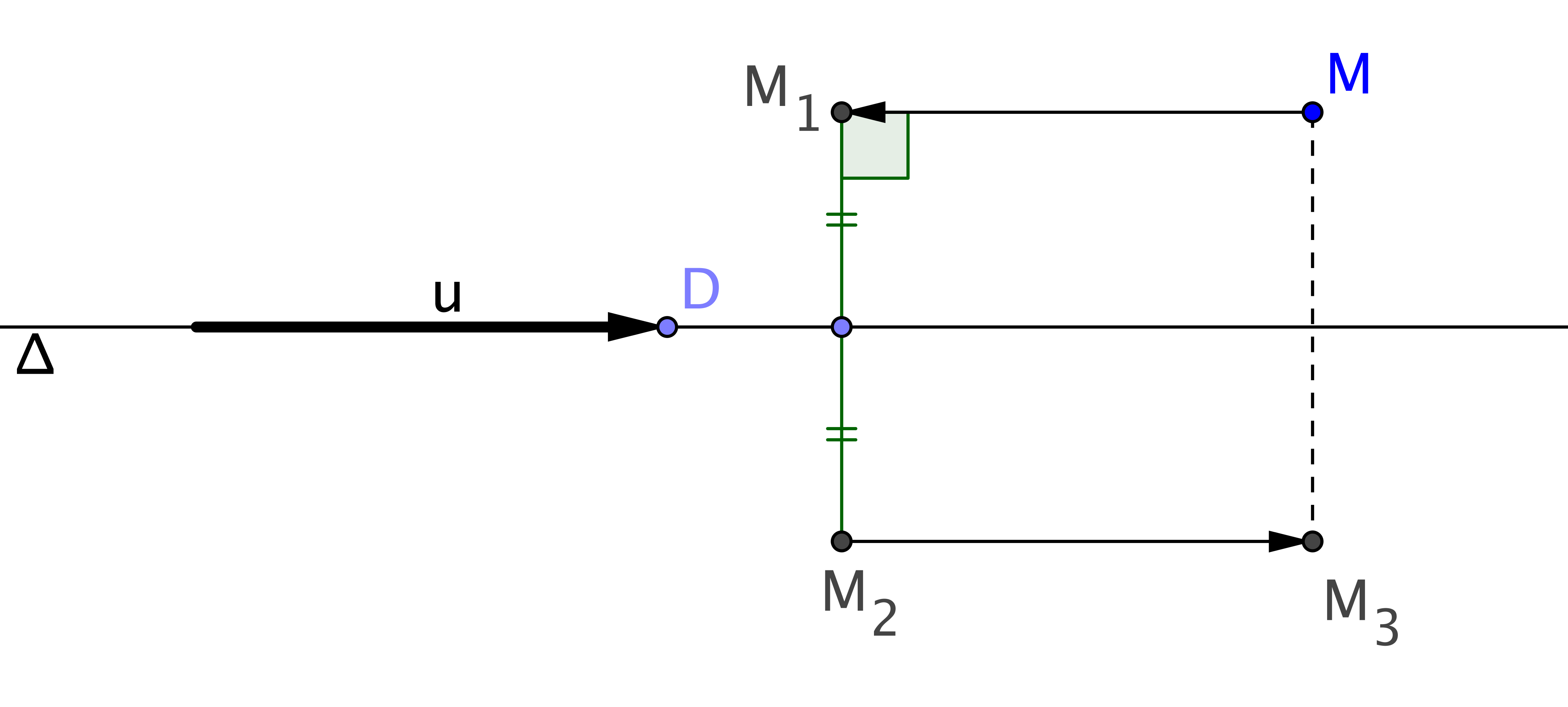
Alors est une médiane puisque parallèle à (M M1) et passant par le milieu de [M1 M2]. Donc le milieu de [M M3] appartient à et (M M3) est perpendiculaire à , ceci signifie que M3 est le symétrique de M par rapport à .
On a donc démontré , qui est équivalent à .
2. En utilisant (1) et le fait qu'une réflexion est involutive, on peut écrire :
3. Le vecteur de la symétrie glissée est uniquement déterminé par l'égalité ; la réflexion est alors uniquement déterminée par .
4. Comme la translation n'admet aucun point fixe, il en est de même pour .
5. Sur la figure, M3 est l'image de M1 par . La droite est une droite des milieux dans le triangle M1 M2 M3 puisque parallèle à la base (M2 M3) et passant par le milieu de [M1 M2] donc elle passe par le milieu N de [M1 M3]. On a donc montré que le milieu N de appartient à pour tout M1.
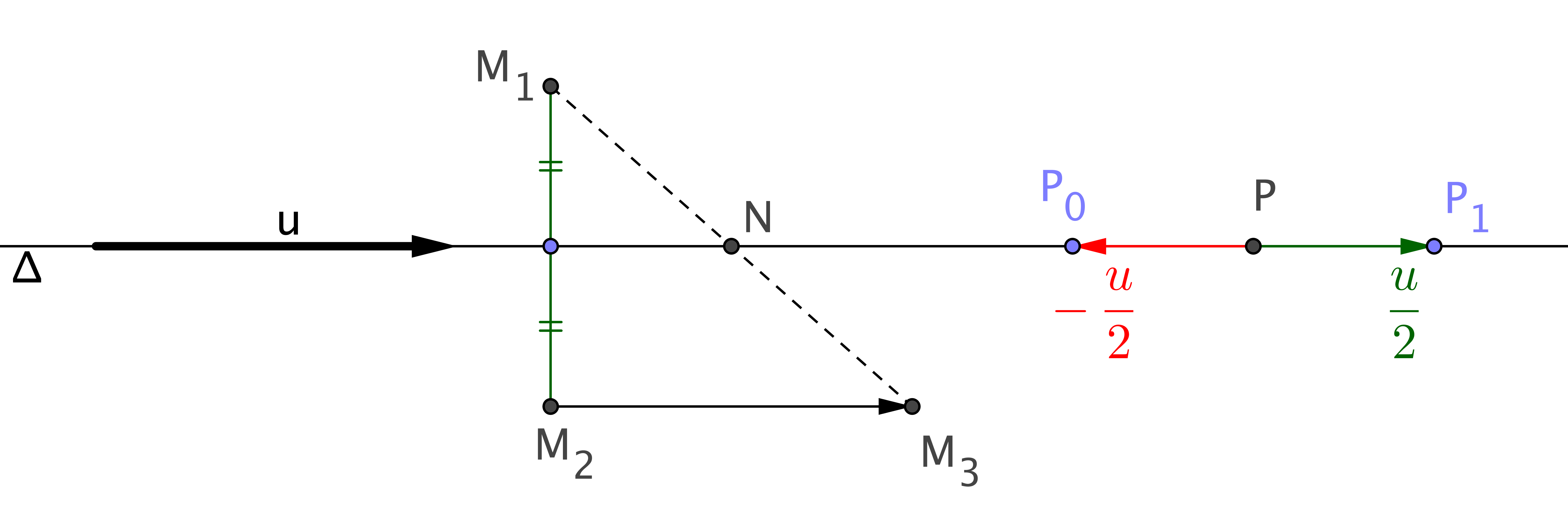 Réciproquement, soit
P un point de
. On pose
et
. Comme
P0 appartient à
, il est fixe par
donc
P1 est l'image par
de
P0 et
P est, par construction, le milieu de
[P0 P1]. On a montré que tout point de
est le milieu d'un segment
pour
M point du plan.
Réciproquement, soit
P un point de
. On pose
et
. Comme
P0 appartient à
, il est fixe par
donc
P1 est l'image par
de
P0 et
P est, par construction, le milieu de
[P0 P1]. On a montré que tout point de
est le milieu d'un segment
pour
M point du plan.
L'assertion (5) est démontrée.
Par l'égalité , le quadrilatère M M1 M2 M3 est un parallélogramme. Comme dirige et que (M1 M2) est perpendiculaire à , l'angle est droit donc M M1 M2 M3 est un rectangle.

Alors est une médiane puisque parallèle à (M M1) et passant par le milieu de [M1 M2]. Donc le milieu de [M M3] appartient à et (M M3) est perpendiculaire à , ceci signifie que M3 est le symétrique de M par rapport à .
On a donc démontré , qui est équivalent à .
2. En utilisant (1) et le fait qu'une réflexion est involutive, on peut écrire :
3. Le vecteur de la symétrie glissée est uniquement déterminé par l'égalité ; la réflexion est alors uniquement déterminée par .
4. Comme la translation n'admet aucun point fixe, il en est de même pour .
5. Sur la figure, M3 est l'image de M1 par . La droite est une droite des milieux dans le triangle M1 M2 M3 puisque parallèle à la base (M2 M3) et passant par le milieu de [M1 M2] donc elle passe par le milieu N de [M1 M3]. On a donc montré que le milieu N de appartient à pour tout M1.

L'assertion (5) est démontrée.
Fin de la démonstration
Exercice
Images de points par une symétrie glissée
Isométries du plan affine euclidien
→
II Exemples d'isométries
→
II-4 Symétrie glissée
→ II-4-2 Propriétés et exercice
II-4-3 Remarques
Isométries du plan affine euclidien
→
II Exemples d'isométries
→
II-4 Symétrie glissée
→ II-4-3 Remarques
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Remarques
- Une symétrie glissée n'est pas une translation sinon on aurait l'égalité entre une translation et une réflexion. Une symétrie glissée n'est ni une réflexion, ni une rotation puisqu'elle n'admet aucun point fixe (voir ici ).
- Une symétrie glissée transforme un angle orienté en son opposé puisqu'elle est la composée d'une réflexion et d'une translation (voir ici et ici )
- Les droites invariantes par une symétrie glissée sont explicitées là .
- En utilisant la décomposition d'une translation comme composée de réflexions d'axes parallèles (voir ici ), on peut montrer la proposition suivante.
Proposition
Dans le plan affine, on considère une droite
 et un vecteur
non nul. Alors
et
commutent si et seulement
dirige
et un vecteur
non nul. Alors
et
commutent si et seulement
dirige
 .
.
 et un vecteur
non nul. Alors
et
commutent si et seulement
dirige
et un vecteur
non nul. Alors
et
commutent si et seulement
dirige
 .
.
Isométries du plan affine euclidien
→
II Exemples d'isométries
→
II-4 Symétrie glissée
→ II-4-3 Remarques
II-5 Rotation
Isométries du plan affine euclidien
→
II Exemples d'isométries
→ II-5 Rotation
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Nous abordons ici le dernier type d'isométrie. Nous avons déjà rencontré une rotation : une symétrie centrale est une rotation d'angle
 . Nous avons déjà composé des réflexions d'axes sécants, mais seulement quand ils étaient perpendiculaires. Nous traitons ici tous les cas.
. Nous avons déjà composé des réflexions d'axes sécants, mais seulement quand ils étaient perpendiculaires. Nous traitons ici tous les cas.
 . Nous avons déjà composé des réflexions d'axes sécants, mais seulement quand ils étaient perpendiculaires. Nous traitons ici tous les cas.
. Nous avons déjà composé des réflexions d'axes sécants, mais seulement quand ils étaient perpendiculaires. Nous traitons ici tous les cas.
Isométries du plan affine euclidien
→
II Exemples d'isométries
→ II-5 Rotation
II-5-1 Définition
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
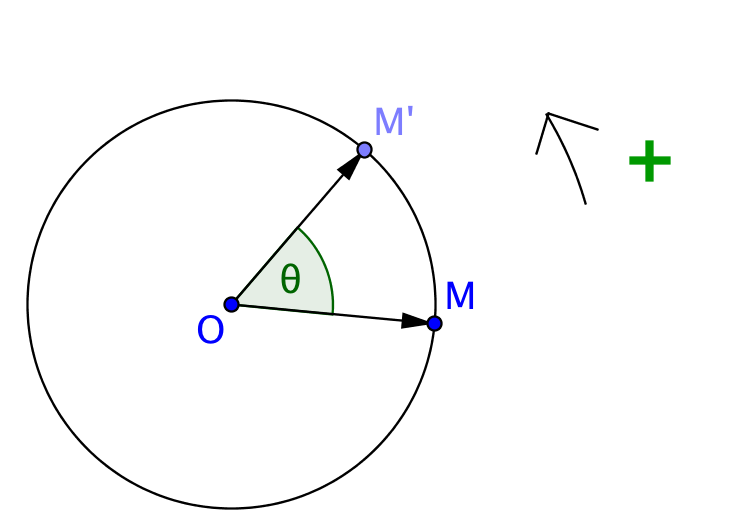
Définition
On appelle rotation de centre
O et d'angle
, et on note
, l'application du plan
dans lui-même qui fixe
O et qui, à
M distinct de
O, associe
M' vérifiant :
- O M = O M'
Exercices
Images de deux points par une rotation
Image d'un triangle par une rotation
Figure mobile pour une rotation.
Sur la figure, le F vert est l'image du F bleu par une rotation d'angle et de sens direct. Vous pouvez déplacer tous les objets rouges.
- II-5-1 Définition
- II-5-2 Composée de deux réflexions d'axes sécants
- II-5-3 Propriétés
- II-5-4 Ordre d'une rotation
II-5-2 Composée de deux réflexions d'axes sécants
Isométries du plan affine euclidien
→
II Exemples d'isométries
→
II-5 Rotation
→ II-5-2 Composée de deux réflexions d'axes sécants
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Proposition
Soient
 et
deux droites sécantes en
O alors
est la rotation de centre
O et d'angle
.
et
deux droites sécantes en
O alors
est la rotation de centre
O et d'angle
.
Réciproquement, si est une droite donnée passant par
O, on peut écrire
comme la composée
où
est la droite image de
est une droite donnée passant par
O, on peut écrire
comme la composée
où
est la droite image de
 par la rotation de centre
O et d'angle
:
.
par la rotation de centre
O et d'angle
:
.
 et
deux droites sécantes en
O alors
est la rotation de centre
O et d'angle
.
et
deux droites sécantes en
O alors
est la rotation de centre
O et d'angle
.
Réciproquement, si
 est une droite donnée passant par
O, on peut écrire
comme la composée
où
est la droite image de
est une droite donnée passant par
O, on peut écrire
comme la composée
où
est la droite image de
 par la rotation de centre
O et d'angle
:
.
par la rotation de centre
O et d'angle
:
.
Démonstration
Remarquons d'abord que
est une isométrie qui fixe
O, on a donc :
OM=OM' pour
.
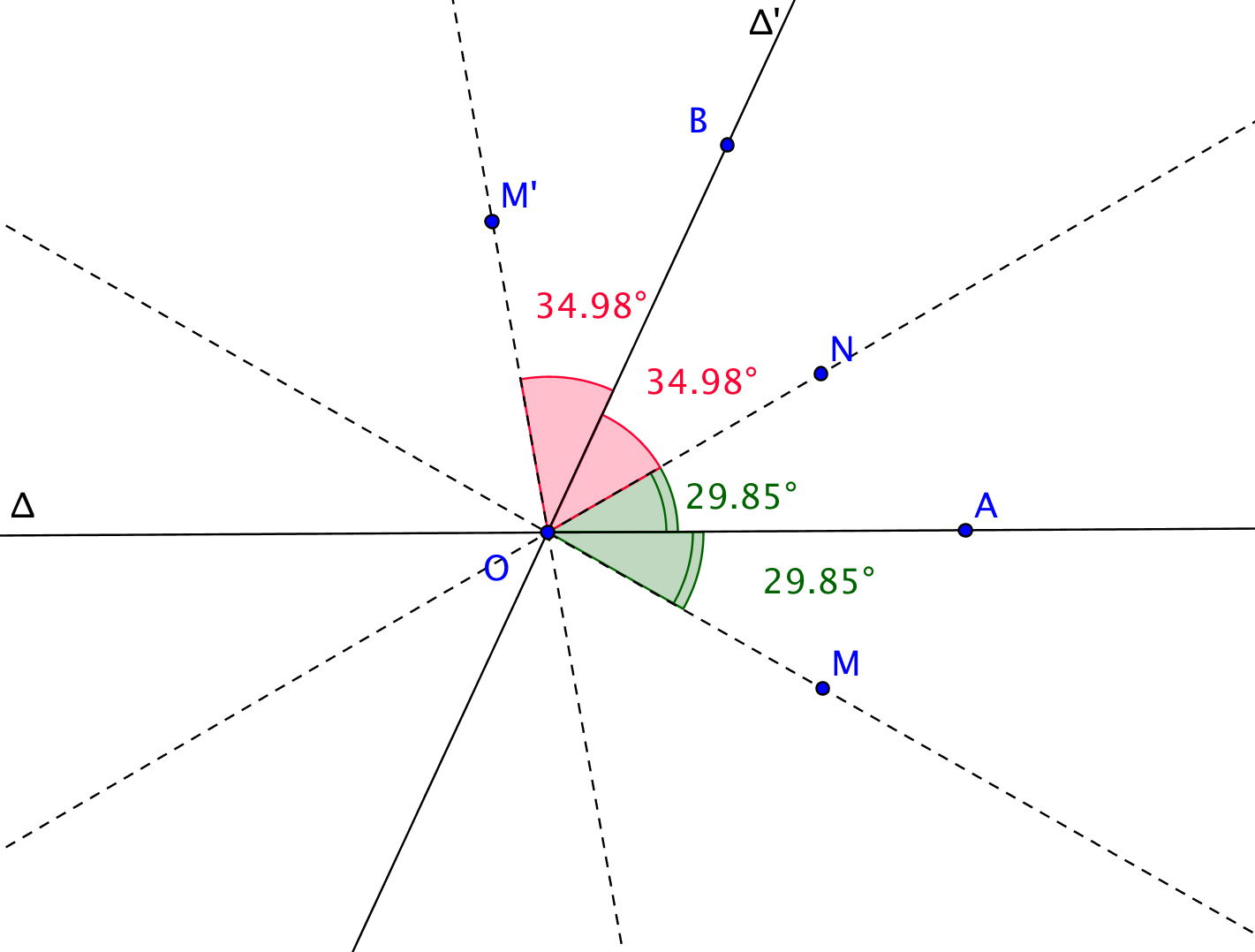
Il reste à calculer l'angle . On note et on considère A (resp. B) un point de (resp.
) distinct de
O. Comme une réflexion transforme un angle orienté en son opposé (voir
ici
), on peut écrire à l'aide de la relation de Chasles :
(resp.
) distinct de
O. Comme une réflexion transforme un angle orienté en son opposé (voir
ici
), on peut écrire à l'aide de la relation de Chasles :
Il reste à calculer l'angle . On note et on considère A (resp. B) un point de
 (resp.
) distinct de
O. Comme une réflexion transforme un angle orienté en son opposé (voir
ici
), on peut écrire à l'aide de la relation de Chasles :
(resp.
) distinct de
O. Comme une réflexion transforme un angle orienté en son opposé (voir
ici
), on peut écrire à l'aide de la relation de Chasles :
Fin de la démonstration
Exercice
Rotation : produit de réflexions
- II-5-1 Définition
- II-5-2 Composée de deux réflexions d'axes sécants
- II-5-3 Propriétés
- II-5-4 Ordre d'une rotation
Isométries du plan affine euclidien
→
II Exemples d'isométries
→
II-5 Rotation
→ II-5-2 Composée de deux réflexions d'axes sécants
II-5-3 Propriétés
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Proposition
- Une rotation est une isométrie.
- Pour tout point O, la rotation de centre O et d'angle 0 est l'identité.
- La rotation de centre O et d'angle est la symétrie centrale de centre O.
- La composée de et est .
- L'inverse de est .
Démonstration
- Une rotation est une isométrie comme composée de deux réflexions.
- Les égalités OM=OM' et sont équivalentes à M=M' donc toute rotation d'angle nul est l'identité.
- Comme on a , la rotation est, par définition, la symétrie centrale de centre O.
- Posons
alors
r fixe
O et pour
M un point du plan distinct de
O, posons
et
. On a alors par définition et relation de Chasles des angles orientés :
- OM=OM'=OM''
- se déduit de (4) ou de la définition.
Fin de la démonstration
Remarque
- II-5-1 Définition
- II-5-2 Composée de deux réflexions d'axes sécants
- II-5-3 Propriétés
- II-5-4 Ordre d'une rotation
II-5-4 Ordre d'une rotation
Isométries du plan affine euclidien
→
II Exemples d'isométries
→
II-5 Rotation
→ II-5-4 Ordre d'une rotation
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Si
est une application et
k un entier naturel non nul, on note
la composée de
k applications égales à
. Par extension, on dit
est l'identité.
Définition
On dit qu'une rotation
est d'ordre fini s'il existe un entier naturel
k non nul tel que
est l'identité. L'ordre de
est alors le plus petit entier naturel
n non nul tel que
est l'identité.
Exemples
Une involution est d'ordre
2.
La rotation
est d'ordre
n.
Exercice
Ordre d'une rotation conservant un végétal
.
- II-5-1 Définition
- II-5-2 Composée de deux réflexions d'axes sécants
- II-5-3 Propriétés
- II-5-4 Ordre d'une rotation
Isométries du plan affine euclidien
→
II Exemples d'isométries
→
II-5 Rotation
→ II-5-4 Ordre d'une rotation
III Isométries et angles
Isométries du plan affine euclidien
→ III Isométries et angles
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Nous allons préciser l'action des quelques isométries sur les angles géométriques ou orientés. La décomposition de isométries en produit de réflexions nous permettra de traiter toutes les isométries.
Isométries du plan affine euclidien
→ III Isométries et angles
III-1 Translations et symétries centrales
Isométries du plan affine euclidien
→
III Isométries et angles
→ III-1 Translations et symétries centrales
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Proposition
Les symétries centrales et les translations conservent les angles orientés de vecteurs.
Démonstration
Soit
une symétrie centrale ou une translation. Soient
O,
A et
B trois points distincts et
O',
A' et
B' leurs images respectives par
.
On a vu que si
est une translation, on a les égalités :
et
; on en déduit :
Si
est une symétrie centrale, on a les égalités :
et
; on en déduit :
Fin de la démonstration
Isométries du plan affine euclidien
→
III Isométries et angles
→ III-1 Translations et symétries centrales
III-3 Exercices
Isométries du plan affine euclidien
→
III Isométries et angles
→ III-3 Exercices
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Ces trois exercices testent les propriétés de certaines isométries.
- Test des translations, symétries centrales et réflexions :
Propriétés d'une isométrie (1) - Test des translations, symétries centrales, réflexions et symétries glissées :
Propriétés d'une isométrie (2) - Test des translations, symétries centrales, réflexions, symétries glissées et rotations :
Propriétés d'une isométrie (3)
Isométries du plan affine euclidien
→
III Isométries et angles
→ III-3 Exercices
IV Droites invariantes par des isométries
Isométries du plan affine euclidien
→ IV Droites invariantes
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Nous déterminons dans cette partie quelles droites sont invariantes par chaque type d'isométrie.
On a vu que l'image d'une droite (A B) par est la droite ; pour décider si (A B) est invariante, il suffit donc de chercher à quelle condition et appartiennent à (A B).
Définition
On dit qu'une droite est invariante par une isométrie
, si elle est égale à son image par
.
On a vu que l'image d'une droite (A B) par est la droite ; pour décider si (A B) est invariante, il suffit donc de chercher à quelle condition et appartiennent à (A B).
Remarque
Une droite fixe point par point est invariante, la réciproque est fausse. Ceci est illustré par l'exemple de la translation qui n'a aucun point fixe mais une infinité de droites invariantes.
Isométries du plan affine euclidien
→ IV Droites invariantes
IV-1 Translation
Isométries du plan affine euclidien
→
IV Droites invariantes
→ IV-1 Translation
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Proposition
Soit un vecteur
non nul.
Une droite
est invariante par
si et seulement si elle est dirigée par
.
Démonstration
Soit une droite
dirigée par
alors si
M appartient à
, le point
appartient à
puisqu'on a
. Donc
est invariante.
Réciproquement, si une droite (AB) est invariante par , alors appartient à (AB) et le vecteur dirige (AB).
Réciproquement, si une droite (AB) est invariante par , alors appartient à (AB) et le vecteur dirige (AB).
Fin de la démonstration
Isométries du plan affine euclidien
→
IV Droites invariantes
→ IV-1 Translation
IV-2 Symétrie centrale
Isométries du plan affine euclidien
→
IV Droites invariantes
→ IV-2 Symétrie centrale
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Proposition
Les droites invariantes par une symétrie centrale sont les droites passant par son centre.
Démonstration
Soit
C un point du plan. Pour tout
M un point du plan, on note
alors
C appartient à la droite
(MM'). Donc les droites invariantes par
sont celles passant par
C.
Fin de la démonstration
Isométries du plan affine euclidien
→
IV Droites invariantes
→ IV-2 Symétrie centrale
IV-3 Réflexion
Isométries du plan affine euclidien
→
IV Droites invariantes
→ IV-3 Réflexion
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Proposition
Soit
une droite du plan. Les droites invariantes par
sont
et les droites perpendiculaires à
.
Démonstration
La droite
est invariante par
puisque fixe point par point.
Soit une droite distincte de et B un point de n'appartenant pas à et B' son image .
Si est invariante par , alors B' appartient à qui est donc confondue avec (BB') et, par définition de , perpendiculaire à
Réciproquement, si perpendiculaire à , par définition, pour tout B de , son image B' appartient à donc est invariante.
Soit une droite distincte de et B un point de n'appartenant pas à et B' son image .
Si est invariante par , alors B' appartient à qui est donc confondue avec (BB') et, par définition de , perpendiculaire à
Réciproquement, si perpendiculaire à , par définition, pour tout B de , son image B' appartient à donc est invariante.
Fin de la démonstration
Isométries du plan affine euclidien
→
IV Droites invariantes
→ IV-3 Réflexion
IV-4 Symétrie glissée
Isométries du plan affine euclidien
→
IV Droites invariantes
→ IV-4 Symétrie glissée
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Proposition
La seule droite invariante par la symétrie glissée
(avec
vecteur non nul dirigeant
) est son axe
.
Démonstration
Si la droite
 est invariante par
alors elle est invariante par
donc elle est dirigée par
et invariante par
. C'est donc l'axe
de
et cet axe est évidemment invariant.
est invariante par
alors elle est invariante par
donc elle est dirigée par
et invariante par
. C'est donc l'axe
de
et cet axe est évidemment invariant.
 est invariante par
alors elle est invariante par
donc elle est dirigée par
et invariante par
. C'est donc l'axe
de
et cet axe est évidemment invariant.
est invariante par
alors elle est invariante par
donc elle est dirigée par
et invariante par
. C'est donc l'axe
de
et cet axe est évidemment invariant.
Fin de la démonstration
Isométries du plan affine euclidien
→
IV Droites invariantes
→ IV-4 Symétrie glissée
IV-5 Rotation
Isométries du plan affine euclidien
→
IV Droites invariantes
→ IV-5 Rotation
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Proposition
Une rotation qui admet une droite invariante est une symétrie centrale ou l'identité.
Démonstration
Soit
une droite.
Comme
ici
, décomposons
en produit de réflexions:
avec
. Si la droite
est invariante par
, alors, comme elle est fixe par
, elle est invariante par
. Deux cas peuvent se présenter :
- La droite
est confondue avec
 et
est l'identité.
et
est l'identité.
- La droite
est perpendiculaire à
 et
est une symétrie centrale comme composée de deux réflexions d'axes perpendiculaires.
et
est une symétrie centrale comme composée de deux réflexions d'axes perpendiculaires.
Fin de la démonstration
Isométries du plan affine euclidien
→
IV Droites invariantes
→ IV-5 Rotation
V Composées d'isométries
Isométries du plan affine euclidien
→ V Composées d'isométries
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
On rassemble ici les résultats concernant la composée de deux isométries. On verra
ici
ce qu'est un groupe. Ces résultats peuvent être démontrés en utilisant l'écriture complexe des transformations (voir le document
Géométrie du plan complexe
).
Ces résultats suivants sont utiles pour déterminer la composée de deux isométries. Il suffit, en effet, de les décomposer en produit de réflexions bien choisies pour que la composée se simplifie. On trouvera des exemples ici et là .
V-1 Groupe des translations et symétries centrales
Ces résultats suivants sont utiles pour déterminer la composée de deux isométries. Il suffit, en effet, de les décomposer en produit de réflexions bien choisies pour que la composée se simplifie. On trouvera des exemples ici et là .
V-2 Composée de deux réflexions
Isométries du plan affine euclidien
→ V Composées d'isométries
V-1 Groupe des translations et symétries centrales
Isométries du plan affine euclidien
→
V Composées d'isométries
→ V-1 Groupe des translations et symétries centrales
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
- V-1 Groupe des translations et symétries centrales
- V-2 Composée de deux réflexions
- V-3 Composée d'une réflexion et d'une translation
- V-4 Principe de conjugaison
Isométries du plan affine euclidien
→
V Composées d'isométries
→ V-1 Groupe des translations et symétries centrales
V-1-1 Proposition
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Proposition
L'ensemble
des translations et symétries centrales muni de la composition est un groupe non commutatif. Plus précisément, si
et
sont des vecteurs et
A,
B et
C des points, on a démontré :
- La composition est une loi interne non commutative :
(i) La composée de deux translations est une translation :(ii) La composée de deux symétries centrales est une translation :(iii) La composée d'une symétrie centrale et d'une translation est une symétrie centrale.
On remarque que et sont différents si est non nul.
- L'élément neutre est l'application identique du plan affine noté :
- L'inverse de est et est son propre inverse.
La démonstration est à la page suivante. Ensuite, une remarque donne des astuces pour mémoriser ces résultats.
V-1-2 Démonstration du 1 de la proposition
Isométries du plan affine euclidien
→
V Composées d'isométries
→
V-1 Groupe des translations et symétries centrales
→ V-1-2 Démonstration du 1 de la proposition
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Les figures mobiles sont dans des plis. Le point M et les données des transformations sont mobiles.
(i) Pour un point M quelconque du plan, on note M' l'image de M par et M'' celle de M' par . Alors, par définition, on a : et , on obtient par la relation de Chasles :
L'application qui à M associe M'' est donc .
(ii) Pour un point M quelconque du plan, on note M' l'image de M par et M'' celle de M' par . Alors, par définition, on a : et , on obtient par la relation de Chasles :
L'application qui à M associe M'' est donc .
Figure : composée de deux symétries centrales
(iii) D'après (b), le point D vérifiant est le point D défini par , c'est-à-dire . En composant à droite par l'égalité , on obtient .
Comme est l'inverse de , la symétrie centrale a pour centre E avec .
Figure : composée d'une symétrie centrale et d'une translation
Isométries du plan affine euclidien
→
V Composées d'isométries
→
V-1 Groupe des translations et symétries centrales
→ V-1-2 Démonstration du 1 de la proposition
V-1-3 Remarque
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Comment mémoriser les éléments caractéristiques des composées ?
Quand on se souvient que la composée est une translation, il suffit d'appliquer à A pour obtenir le vecteur de la translation composée:
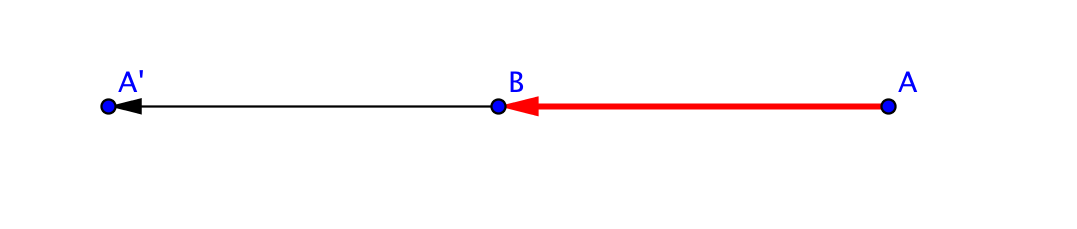
Quand on se souvient que la composée est une symétrie centrale, il suffit d'appliquer à A pour obtenir le centre C de la symétrie composée :

V-2 Composée de deux réflexions
Isométries du plan affine euclidien
→
V Composées d'isométries
→ V-2 Composée de deux réflexions
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Selon que les axes des deux réflexions sont parallèles ou non, la composée sera une translation ou une rotation.
- V-1 Groupe des translations et symétries centrales
- V-2 Composée de deux réflexions
- V-3 Composée d'une réflexion et d'une translation
- V-4 Principe de conjugaison
Isométries du plan affine euclidien
→
V Composées d'isométries
→ V-2 Composée de deux réflexions
V-2-1 Les axes sont parallèles
Isométries du plan affine euclidien
→
V Composées d'isométries
→
V-2 Composée de deux réflexions
→ V-2-1 Les axes sont parallèles
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Proposition
Soient
et
deux droites parallèles et
une perpendiculaire commune à
en
N1 et à
en
N2. La composée
est la translation de vecteur
.
Soit une translation de vecteur et une droite quelconque orthogonale à
. Alors on peut décomposer
en produit de deux réflexions
où
est l'image de
une droite quelconque orthogonale à
. Alors on peut décomposer
en produit de deux réflexions
où
est l'image de
 par la translation
:
par la translation
:
Soit une translation de vecteur et
 une droite quelconque orthogonale à
. Alors on peut décomposer
en produit de deux réflexions
où
est l'image de
une droite quelconque orthogonale à
. Alors on peut décomposer
en produit de deux réflexions
où
est l'image de
 par la translation
:
par la translation
:
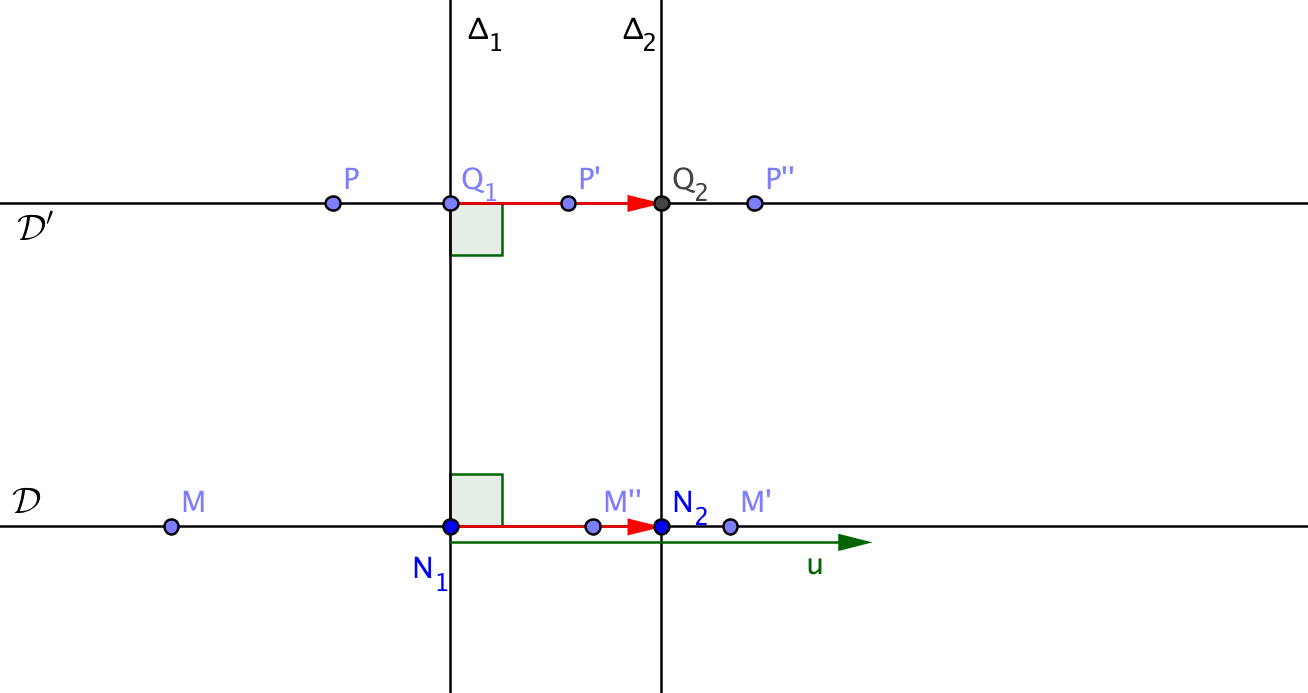
Démonstration
Soit
M un point du plan,
N1 et
N2 ses projetés orthogonaux sur
et
. On note
et
. Alors, par définition de la projection et de la réflexion, les points
M,
M',
M'',
N1 et
N2 sont alignés sur la perpendiculaire commune
à
et
passant par
M. La restriction de
à
est égale à
, c'est-à-dire à la translation de vecteur
.
Pour une autre perpendiculaire commune à et passant par un point P, la restriction de à est égale à la translation de vecteur (avec les notations de la figure).
Comme les côtés opposés de N1 N2 Q2 Q1 sont parallèles, N1 N2 Q2 Q1 est un parallélogramme donc les vecteurs et sont égaux. On a donc montré que est égale à la translation de vecteur et que ce vecteur ne dépend pas de la perpendiculaire commune à et .
Pour une autre perpendiculaire commune à et passant par un point P, la restriction de à est égale à la translation de vecteur (avec les notations de la figure).
Comme les côtés opposés de N1 N2 Q2 Q1 sont parallèles, N1 N2 Q2 Q1 est un parallélogramme donc les vecteurs et sont égaux. On a donc montré que est égale à la translation de vecteur et que ce vecteur ne dépend pas de la perpendiculaire commune à et .
Fin de la démonstration
Remarque
On peut donc écrire une symétrie glissée comme composée de trois réflexions.
Isométries du plan affine euclidien
→
V Composées d'isométries
→
V-2 Composée de deux réflexions
→ V-2-1 Les axes sont parallèles
V-2-2 Les axes sont sécants
Isométries du plan affine euclidien
→
V Composées d'isométries
→
V-2 Composée de deux réflexions
→ V-2-2 Les axes sont sécants
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Proposition
Soient
et
deux droites perpendiculaires et
A leur point d'intersection. La composée
est la symétrie centrale de centre
A. Elle est égale à
.
Démonstration
Ce résultat est un cas particulier de cette
proposition
. On peut aussi le démontrer directement en se plaçant dans le cas particulier où les axes des réflexions sont les axes de coordonnées.
Fin de la démonstration
On rappelle cette proposition vue ici .
Proposition
La composée de deux réflexions d'axes sécants est une rotation. Toute rotation peut se decomposer comme produit de deux réflexions dont l'une est donnée.
Isométries du plan affine euclidien
→
V Composées d'isométries
→
V-2 Composée de deux réflexions
→ V-2-2 Les axes sont sécants
V-3 Composée d'une réflexion et d'une translation
Isométries du plan affine euclidien
→
V Composées d'isométries
→ V-3 Composée d'une réflexion et d'une translation
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Dans le plan muni d'un repère orthonormé, considérons un vecteur
et une droite
dirigée par un vecteur
. Le but de cette partie est de déterminer l'isométrie
.
Décomposons le vecteur selon la direction de et la direction orthogonale, c'est-à-dire écrivons où est un réel et un vecteur orthogonal à . Cette décomposition est unique. Posons .
La décomposition d'une translation vue ici nous donne : avec . On en déduit :
Comme la droite
est parallèle à
dirigée par
, l'isométrie
est une symétrie glissée d'axe
et de vecteur
.
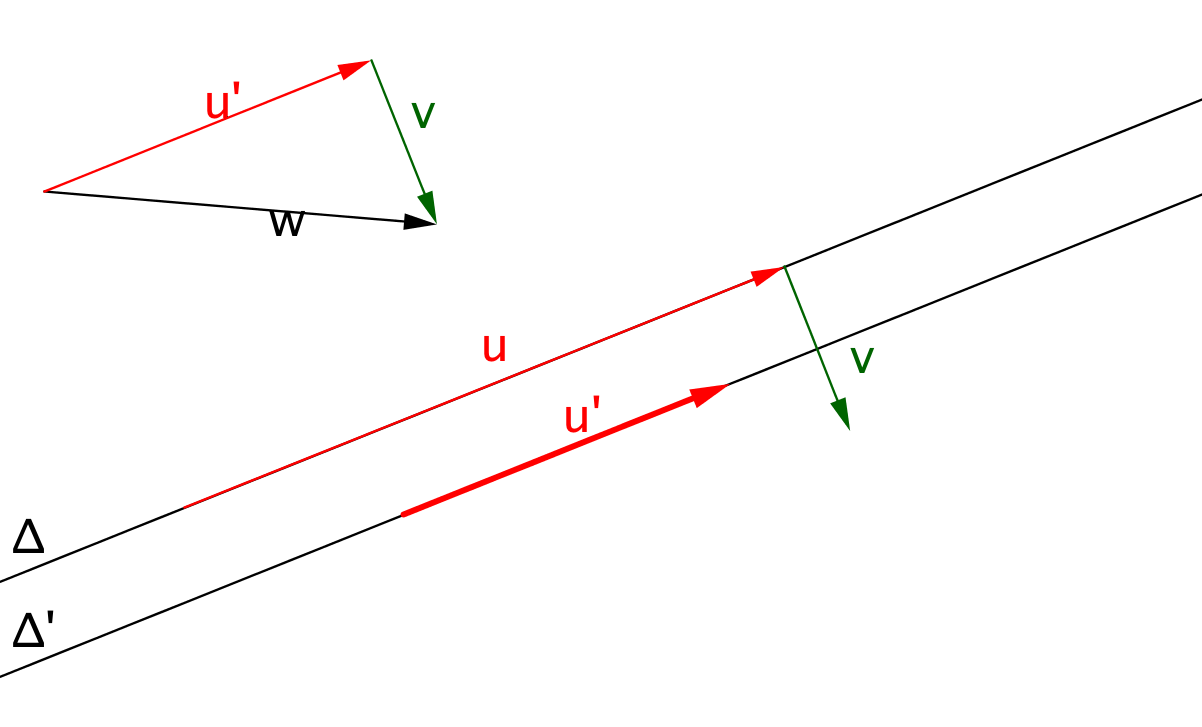
Décomposons le vecteur selon la direction de et la direction orthogonale, c'est-à-dire écrivons où est un réel et un vecteur orthogonal à . Cette décomposition est unique. Posons .
La décomposition d'une translation vue ici nous donne : avec . On en déduit :

Exercices
Ces exercices sont des applications directes de cette étude.
Composition translation et réflexion (1) (exercice graphique)
Composition translation et réflexion (2) (exercice graphique)
Composée translation et réflexion (3) (exercice graphique)
Composée d'une réflexion et d'une translation (1) (version analytique)
Composée d'une réflexion et d'une translation (2) (version analytique)
Composition translation et réflexion (1) (exercice graphique)
Composition translation et réflexion (2) (exercice graphique)
Composée translation et réflexion (3) (exercice graphique)
Composée d'une réflexion et d'une translation (1) (version analytique)
Composée d'une réflexion et d'une translation (2) (version analytique)
- V-1 Groupe des translations et symétries centrales
- V-2 Composée de deux réflexions
- V-3 Composée d'une réflexion et d'une translation
- V-4 Principe de conjugaison
Isométries du plan affine euclidien
→
V Composées d'isométries
→ V-3 Composée d'une réflexion et d'une translation
V-4 Principe de conjugaison
Isométries du plan affine euclidien
→
V Composées d'isométries
→ V-4 Principe de conjugaison
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Le principe de conjugaison est utile pour décider si deux isométries commutent ou non. Dans ce cadre, on compose trois isométries.
- V-1 Groupe des translations et symétries centrales
- V-2 Composée de deux réflexions
- V-3 Composée d'une réflexion et d'une translation
- V-4 Principe de conjugaison
Isométries du plan affine euclidien
→
V Composées d'isométries
→ V-4 Principe de conjugaison
V-4-1 Définitions et propriétés
Isométries du plan affine euclidien
→
V Composées d'isométries
→
V-4 Principe de conjugaison
→ V-4-1 Définitions et propriétés
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Définition
Soient
f et
g des applications.
On appelle conjugué de
g par
f l'application
.
Remarque
Si
est le conjugué de
g par
f, alors
g est le conjugué de
par
. Il suffit d'écrire :
Proposition [Points fixes]
Les points fixes de
sont les images par
f des points fixes de
g.
Démonstration
Posons
. Notons
Fixes(g) (resp.
l'ensemble des points fixes de
g (resp.
). Nous voulons montrer l'égalité :
.
Soit C un point fixe de g. Par un calcul direct, on constate que l'image de f(C) par est f(C). Donc nous avons montré l'inclusion .
Appliquons ce résultat à g qui est le conjugué de de par . Nous obtenons l'inclusion , c'est-à-dire .
Les deux inclusions donnent l'égalité attendue.
Soit C un point fixe de g. Par un calcul direct, on constate que l'image de f(C) par est f(C). Donc nous avons montré l'inclusion .
Appliquons ce résultat à g qui est le conjugué de de par . Nous obtenons l'inclusion , c'est-à-dire .
Les deux inclusions donnent l'égalité attendue.
Fin de la démonstration
Proposition
Le conjugué d'une involution est une involution.
Démonstration
Si
s est une involution, alors, comme
est égal à l'identité, on a :
Fin de la démonstration
Ces propriétés suggèrent le principe de conjugaison :
Corollaire [Principe de conjugaison]
Le conjugué d'une isométrie
g est une isométrie de même type que
g dont les éléments caractéristiques sont les "images par
f" de ceux de
g.
Ce résultat doit être démontré dans chaque cas. Comme on connaît le type du conjugué, la démonstration s'avère plus facile.En effet, dans la plupart des cas, le nombre de points fixes caractérise le type d'une isométrie dès qu'on sait si elle est positive ou négative (voir ici et ici ). Une isométrie et sa conjuguée ont même nombre de points fixes et même "signe". Seul le cas des rotations demande un peu plus de travail.
Isométries du plan affine euclidien
→
V Composées d'isométries
→
V-4 Principe de conjugaison
→ V-4-1 Définitions et propriétés
V-4-2 Applications
Isométries du plan affine euclidien
→
V Composées d'isométries
→
V-4 Principe de conjugaison
→ V-4-2 Applications
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Exemple
Soit
un vecteur non nul et
A un point du plan. L'isométrie
la symétrie centrale de centre
.
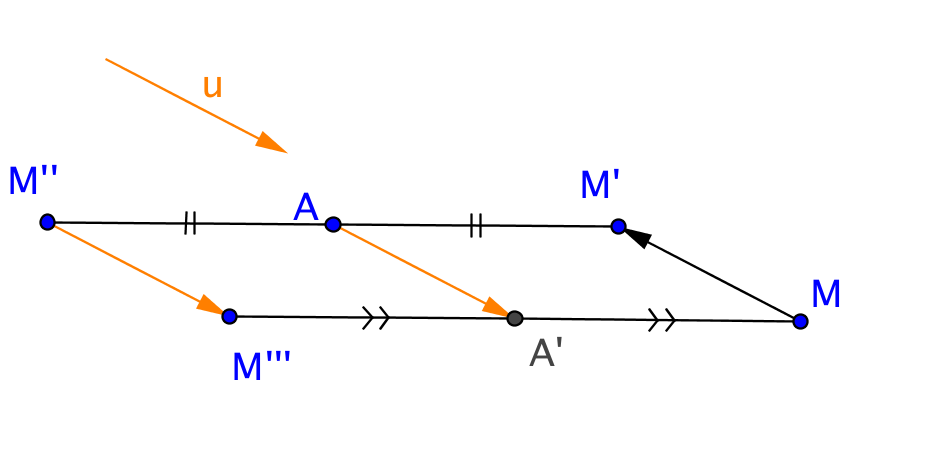
Démonstration
Première méthode. On sait que la composée d'une symétrie centrale et d'une translation est une symétrie centrale donc
est une symétrie centrale qui composée avec
donne une autre symétrie centrale dont le centre est son unique point fixe
.
Deuxième méthode. Quand on connaît la classification des isométries (voir ici , on sait que est une isométrie positive, de plus c'est une involution avec comme unique point fixe est , est donc la symétrie centrale de centre .
Deuxième méthode. Quand on connaît la classification des isométries (voir ici , on sait que est une isométrie positive, de plus c'est une involution avec comme unique point fixe est , est donc la symétrie centrale de centre .
Fin de la démonstration
Exemple
Soit
un vecteur non nul. L'isométrie
est un antidéplacement qui fixe point par point la droite
, c'est donc la réflexion d'axe
.
On pouvait aussi conclure en utilisant simplement le lemme du théorème de décomposition. Comme admet au moins deux points fixes (des points de ) et n'est pas l'identité, elle est la réflexion d'axe .
On pouvait aussi conclure en utilisant simplement le lemme du théorème de décomposition. Comme admet au moins deux points fixes (des points de ) et n'est pas l'identité, elle est la réflexion d'axe .
Remarque
Le principe de conjugaison est très utile dans les questions de commutation. Il est clair que deux applications
f et
g commutent si et seulement si le conjugué de
g par
f est l'application
g.
Par exemple, puisque est la symétrie centrale de centre , une translation et une symétrie centrale ne commutent pas sauf si le vecteur de la translation est nul.
Par exemple, puisque est la symétrie centrale de centre , une translation et une symétrie centrale ne commutent pas sauf si le vecteur de la translation est nul.
Isométries du plan affine euclidien
→
V Composées d'isométries
→
V-4 Principe de conjugaison
→ V-4-2 Applications
VI Décomposition en produit de réflexions.
Isométries du plan affine euclidien
→ VI Décomposition en produit de réflexions.
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
L'identité est composée de zéro réflexion par convention. Les translations et les rotations sont composées de deux réflexions. Les réflexions sont composées d'une seule réflexion et les symétries glissées de trois (on décompose la translation en produit de deux réflexions.). Le théorème présenté ici affirme que toute isométrie peut être décomposée en produit de réflexions. Il a une grande importance théorique (voir les propriétés des isométries ici ) mais aussi pratique (voir l'exemple ici et l'application là ).
A la suite de ce théorème, nous admettons que nous avons ainsi vu tous les types d'isométries.
Isométries du plan affine euclidien
→ VI Décomposition en produit de réflexions.
VI-1 Théorème
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Théorème
Toute isométrie du plan est la composée d'au plus trois réflexions.
La démonstration se déroule en plusieurs lemmes.
Lemme
Si une isométrie
fixe trois points non alignés
A,
B et
C, alors
est l'identité.
Démonstration
En effet si
est distinct de
M alors puisque
est une isométrie, on a :
A M = A M',
B M = B M' et
C M = C M', les trois points
A,
B et
C sont donc alignés sur la médiatrice de
[M M'].
Fin de la démonstration
Remarque
Ce lemme pourrait s'énoncer ainsi : Soit
une isométrie fixant
trois points
A,
B et
C. Si
A,
B et
C ne sont pas alignés, alors
est l'identité.
On a démontré la contraposée de cette proposition : Si
n'est pas l'identité alors
A,
B et
C sont alignés sur la médiatrice de
pour
.
Parmi les isométries que nous connaissons, celles qui ont trois points fixes distincts sont des réflexions. L'axe d'une réflexion est de fait la médiatrice de pour .
Parmi les isométries que nous connaissons, celles qui ont trois points fixes distincts sont des réflexions. L'axe d'une réflexion est de fait la médiatrice de pour .
Lemme
Démonstration
En effet soit
C n'appartenant pas à la droite
(AB) tel que
soit distinct de
C, alors comme
est une isométrie et que
A et
B sont fixes par
, on a :
A C = A C' et
B C = B C' donc
(A B) est la médiatrice de
[C C']. L'application
fixe trois points non alignés
A,
B et
C, c'est donc l'identité et
égale
.
Fin de la démonstration
Lemme
Si une isométrie
admet un unique point fixe
A, alors
est une rotation de centre
A, composée de deux réflexions.
Démonstration
En effet soit
B distinct de
A et
B' son image par
(distincte de
B par hypothèse). Comme
est une isométrie,
A appartient à la médiatrice
de
[B B']. Alors
fixe
A et
B (deux points distincts) donc cette isométrie est l'identité (impossible car
serait une réflexion) ou une réflexion d'axe
(A B). Donc
la composée de deux réflexions d'axes passant par
A,
est une rotation de centre
A.
Fin de la démonstration
Lemme
Si une isométrie
n'admet aucun point fixe, elle est composée d'au plus trois réflexions.
Démonstration
Soit
A et son image
et
la médiatrice de
[A A']. Alors
fixe
A donc est composée d'au plus deux réflexions.
Fin de la démonstration
VI-2 Remarque
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Nous avons déterminé les types des composées de deux réflexions
ici
.
Pour décrire les composées de trois réflexions, nous allons commencer par admettre la proposition suivante.
Une fois ce résultat admis, pour déterminer la composée de trois réflexions, il reste à considérer deux cas : Nous admettrons donc que la composée de trois réflexions est soit une réflexion, soit une symétrie glissée.
Proposition
Soient
,
et
trois droites du plan.
La composée de trois réflexions
est une réflexion si et seulement si les droites
,
et
sont parallèles ou concourantes.
Une fois ce résultat admis, pour déterminer la composée de trois réflexions, il reste à considérer deux cas : Nous admettrons donc que la composée de trois réflexions est soit une réflexion, soit une symétrie glissée.
VI-3 Application
Isométries du plan affine euclidien
→
VI Décomposition en produit de réflexions.
→ VI-3 Application
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Pour simplifier la composée de deux déplacements, il est souvent utile de décomposer chaque isométrie comme produit de deux ou trois réflexions bien choisies. Voici un exemple.
Exemple
Soit un vecteur
et un point
A. On veut déterminer
.
Quel est le type de ? L'isométrie est un déplacement comme composée de déplacements (voir ici ). Ce n'est pas une translation sinon serait une translation ! C'est donc une rotation.
Pour décomposer en réflexions, nous devons utiliser des réflexions d'axes passant par A. Pour décomposer en réflexions, nous devons utiliser des réflexions d'axes orthogonaux à . Soit donc la droite passant par A et orthogonale à .
Alors s'écrit si est la droite passant par A et telle que l'angle soit égal à .
Alors s'écrit si est l'image de par la translation de vecteur .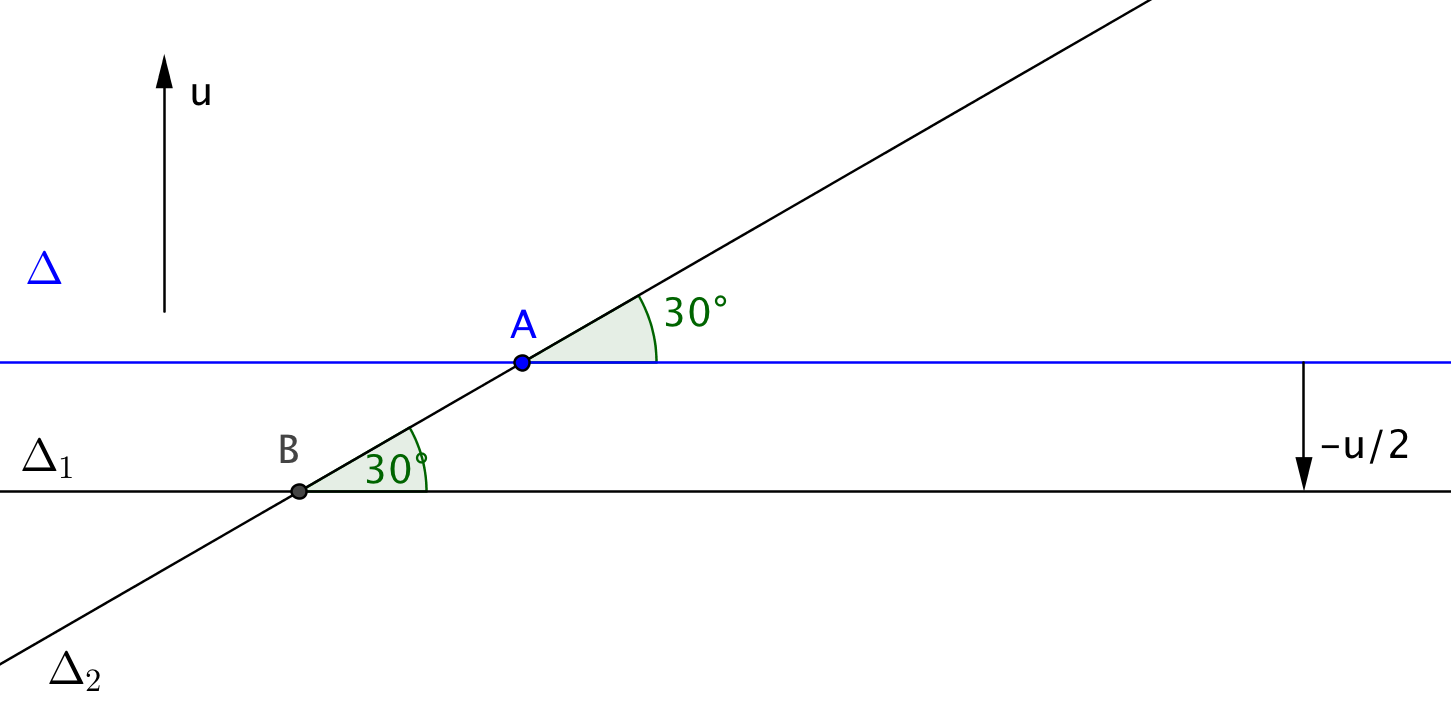 On peut maintenant calculer
:
On peut maintenant calculer
:
Comme est parallèle à , les droites et sont sécantes en un point nommé B et est la rotation de centre B et d'angle .
Quel est le type de ? L'isométrie est un déplacement comme composée de déplacements (voir ici ). Ce n'est pas une translation sinon serait une translation ! C'est donc une rotation.
Pour décomposer en réflexions, nous devons utiliser des réflexions d'axes passant par A. Pour décomposer en réflexions, nous devons utiliser des réflexions d'axes orthogonaux à . Soit donc la droite passant par A et orthogonale à .
Alors s'écrit si est la droite passant par A et telle que l'angle soit égal à .
Alors s'écrit si est l'image de par la translation de vecteur .

Comme est parallèle à , les droites et sont sécantes en un point nommé B et est la rotation de centre B et d'angle .
Exercice
Cet exercice propose le cas plus simple de la composée d'une rotation et d'une réflexion.
Composée rotation - réflexion (exercice graphique)
Composée rotation - réflexion (exercice graphique)
Isométries du plan affine euclidien
→
VI Décomposition en produit de réflexions.
→ VI-3 Application
VII Classification
Isométries du plan affine euclidien
→ VII Classification
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Dans cette partie, les isométries sont présentées en groupe et classées selon leurs propriétés (action sur les angles, points fixes et droites invariantes). Commençons donc par définir le sens mathématique du mot groupe.
Isométries du plan affine euclidien
→ VII Classification
VII-1 Groupe
Isométries du plan affine euclidien
→
VII Classification
→ VII-1 Groupe
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Tout au long de l'enseignement secondaire, on rencontre des groupes sans le savoir ... voir
ici
!
- VII-1 Groupe
- VII-2 Groupe des isométries
- VII-3 Isométries et angles orientés
- VII-4 Caractérisation des isométries
Isométries du plan affine euclidien
→
VII Classification
→ VII-1 Groupe
VII-1-2 Exemples de groupes de nombres
Isométries du plan affine euclidien
→
VII Classification
→
VII-1 Groupe
→ VII-1-2 Exemples de groupes de nombres
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Voici quelques exemples de groupes numériques.
- n'est pas un groupe. Un entier non nul n'a pas de symétrique pour l'addition dans .
- est un groupe commutatif.
- est un groupe commutatif.
- n'est pas un groupe.
- est un groupe commutatif.
- est un groupe commutatif.
Isométries du plan affine euclidien
→
VII Classification
→
VII-1 Groupe
→ VII-1-2 Exemples de groupes de nombres
VII-1-1 Définition
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Définition
On appelle groupe
G un ensemble muni d'une loi de composition interne
(une application qui à deux éléments de
G associe un élément de
G) tels que :
- La loi
soit associative : pour tous
g1,
g2 et
g3 éléments du groupe, on a :
- Il existe dans G un élément neutre e pour la loi : Pour tout ,
- Tout élément g a un inverse (appelé aussi symétrique quand le groupe est commutatif) tel que .
Remarques
- L'addition de nombres réels est commutative.
- La loi de composition des applications est associative mais non commutative en général.
VII-1-3 Exemples de groupes en géométrie
Isométries du plan affine euclidien
→
VII Classification
→
VII-1 Groupe
→ VII-1-3 Exemples de groupes en géométrie
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Exemple
Si
est une réflexion du plan, l'ensemble
est un groupe. En effet
est son propre inverse.
Les propriétés vues ici nous donnent deux autres groupes.
Exemple
Les translations forment un groupe commutatif pour la loi de composition. Ce groupe, noté
, est isomorphe au groupe additif des vecteurs.
Exemple
L'ensemble
muni de la composition est un groupe non commutatif.
Isométries du plan affine euclidien
→
VII Classification
→
VII-1 Groupe
→ VII-1-3 Exemples de groupes en géométrie
VII-2 Groupe des isométries
Isométries du plan affine euclidien
→
VII Classification
→ VII-2 Groupe des isométries
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Théorème
On note
l'ensemble des isométries du plan
.
Alors
est un groupe non commutatif.
Démonstration
Vérifions les trois axiomes d'un groupe.
- La composition est associative, montrons que c'est une loi interne dans l'ensemble des isométries.
La composée de deux isométries est une isométrie. En effet, si
et
sont deux isométries du plan et
M et
N deux points quelconques alors la longueur
M N est conservée par
:
La loi de composition est donc interne dans mais non commutative, par exemple, deux symétries centrales ne commutent pas.
- L'identité est une isométrie.
- Toute isométrie a un inverse qui est une isométrie comme composée de réflexion. Par exemple, si
,
et
sont des droites, l'inverse de
est
en effet on calcule en utilisant l'associativité et le fait qu'une réflexion est involutive :
Fin de la démonstration
Proposition
Une isométrie transforme une droite en une droite, deux droites parallèles en deux droites parallèles et conserve le produit scalaire, les angles géométriques et les milieux.
Démonstration
Ces propriétés sont vérifiées par toutes les isométries puisqu'elles le sont par les réflexions et donc par leurs composées.
Fin de la démonstration
- VII-1 Groupe
- VII-2 Groupe des isométries
- VII-3 Isométries et angles orientés
- VII-4 Caractérisation des isométries
Isométries du plan affine euclidien
→
VII Classification
→ VII-2 Groupe des isométries
VII-3 Isométries et angles orientés
Isométries du plan affine euclidien
→
VII Classification
→ VII-3 Isométries et angles orientés
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
La proposition suivante résulte du fait qu'une réflexion change un angle orienté en son opposé (voir
ici
).
On en déduit la première affirmation de la proposition suivante ; la deuxième affirmation résulte des propriétés vues ici .
Proposition
Une composée d'un nombre pair de réflexions conserve les angles orientés. Une composée d'un nombre impair de réflexions change un angle orienté en son opposé.
La parité du nombre de réflexions dans la décomposition d'une isométrie ne dépend donc pas de la décomposition.
Définition
On dit qu'une isométrie est un déplacement ou une isométrie positive si elle conserve les angles orientés.
Sinon on dit que c'est un antidéplacement ou une isométrie négative.
Sinon on dit que c'est un antidéplacement ou une isométrie négative.
Corollaire
- Un déplacement est une isométrie composée d'un nombre pair de réflexions.
- Un antidéplacement est une isométrie composée d'un nombre impair de réflexions.
- La composée de deux déplacements est un déplacement.
- La composée de deux antidéplacements est un déplacement.
- La composée d'un antidéplacement et d'un déplacement est un antidéplacement.
On en déduit la première affirmation de la proposition suivante ; la deuxième affirmation résulte des propriétés vues ici .
Proposition
On note
l'ensemble des isométries positives du plan
. Alors
est un groupe non commutatif.
Soit C un point, l'ensemble des rotations de centre C muni de la composition est un groupe commutatif.
Soit C un point, l'ensemble des rotations de centre C muni de la composition est un groupe commutatif.
- VII-1 Groupe
- VII-2 Groupe des isométries
- VII-3 Isométries et angles orientés
- VII-4 Caractérisation des isométries
Isométries du plan affine euclidien
→
VII Classification
→ VII-3 Isométries et angles orientés
VIII Faisons agir des isométries
Isométries du plan affine euclidien
→ VIII Faisons agir des isométries
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Pour appliquer les résultats de ce cours et entrer plus avant dans ces notions, il est intéressant de faire agir et de reconnaître les isométries sur des objets un peu riches.
Isométries du plan affine euclidien
→ VIII Faisons agir des isométries
VIII-1 Frises et isométries
Isométries du plan affine euclidien
→
VIII Faisons agir des isométries
→ VIII-1 Frises et isométries
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Quand on connaît les translations, symétries centrales, réflexions et symétries glissées et leurs droites invariantes, qu'on sait les composer, on est outillé pour étudier les isométries d'une frise. Cette étude est l'objet du document
Frises et isométries
. De nombreux exercices sont proposés.
Isométries du plan affine euclidien
→
VIII Faisons agir des isométries
→ VIII-1 Frises et isométries
VIII-2 Polygones et isométries
Isométries du plan affine euclidien
→
VIII Faisons agir des isométries
→ VIII-2 Polygones et isométries
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
Quand on connaît les rotations et les réflexions et qu'on sait les composer, on est outillé pour étudier les polygones réguliers.
Le livre de Daniel Perrin, Mathématiques d'école
Le livre de Daniel Perrin, Mathématiques d'école
Mathématiques d'école : nombres, mesures et géométrie publié par Editions Cassini (402 p. ISBN 978-2-84225-158-1)
présente une étude complète des polygones réguliers, du groupe de leurs isométries et de leur construction à la règle et au compas.
On peut consulter aussi le document
Polygones convexes réguliers
.
Isométries du plan affine euclidien
→
VIII Faisons agir des isométries
→ VIII-2 Polygones et isométries
VIII-3 Pavage et isométries
Isométries du plan affine euclidien
→
VIII Faisons agir des isométries
→ VIII-3 Pavage et isométries
- I Applications du plan affine
- II Exemples d'isométries
- III Isométries et angles
- IV Droites invariantes
- V Composées d'isométries
- VI Décomposition en produit de réflexions.
- VII Classification
- VIII Faisons agir des isométries
On peut aussi faire agir les isométries sur des pavages.
Consultez le document
Frises et pavages
.
Isométries du plan affine euclidien
→
VIII Faisons agir des isométries
→ VIII-3 Pavage et isométries