Arithmétique modulaire

Guide

La première partie de ce document est une introduction de l'anneau

/ n

à partir des congruences.
La deuxième partie met l'accent sur quelques résolutions de problèmes où l'utilisation des congruences est fondamentale ou simplement pratique. Ce document n'a aucune prétention à être complet ni même achevé. On espère qu'il peut être utile ainsi.

Définition et opérations algébriques
- Définition
- Opérations
Inverses et diviseurs de zéro
Résolution de quelques problèmes

Définition et opérations algébriques

Définition
Opérations
- Table de multiplication
- Table d'addition

Définition

Une classe de congruence modulo n est un sous-ensemble de

de la forme

avec a un entier. L'ensemble des classes de congruences modulo n est noté . On note aussi

a + n

= a mod n

Un entier b est appelé un représentant de la classe si b et a sont congrus modulo n.

Exemple :

Les classes 6 + 67 et 140 + 67 sont égales.
Les classes 6 + 67 et 343 + 67 sont différentes.
L'entier 140 est un représentant de la classe 6 mod 67.

On choisit en général les représentants entre 0 et n-1, ce qui est toujours possible.

Le reste de la division euclidienne de a par n est bien un représentant de a mod n qui est compris entre 0 et n-1.

Mais il est quelquefois commode de prendre les représentants entre et et même de les prendre quelconques.

Exercice : Classes

Exemple pour plus tard : Il est quand même plus facile de calculer la puissance k-ième de la classe 592 mod 593 en utilisant le représentant de cette classe qu'est -1. Ainsi :

592^k= (-1)^k mod 593

592²⁸⁹⁴= 1 mod 593

Opérations

On définit les opérations algébriques d'addition, soustraction, multiplication par

Mais nous écrirons souvent a + b mod n, par exemple

13 + 5 mod 53 = 18 mod 53 , 13 times

5 mod 53 = 12 mod 53

et même

13 + 5

18 mod 53 , 13 times

12 mod 53 .

On peut voir ici quelques tables d' addition ou de multiplication.

Théorème :

/ n

est un anneau commutatif.

Exercices : Opérations , Carrés Somme et produit

Table d'addition

Voici la table d'addition dans

+	0	1	2	3	4	5
0	0	1	2	3	4	5
1	1	2	3	4	5	0
2	2	3	4	5	0	1
3	3	4	5	0	1	2
4	4	5	0	1	2	3
5	5	0	1	2	3	4

Table de multiplication

Voici la table de multiplication dans

/11

	1	2	3	4	5	6	7	8	9	10
0	0	0	0	0	0	0	0	0	0	0
1	1	2	3	4	5	6	7	8	9	10
2	2	4	6	8	10	1	3	5	7	9
3	3	6	9	1	4	7	10	2	5	8
4	4	8	1	5	9	2	6	10	3	7
5	5	10	4	9	3	8	2	7	1	6
6	6	1	7	2	8	3	9	4	10	5
7	7	3	10	6	2	9	5	1	8	4
8	8	5	2	10	7	4	1	9	6	3
9	9	7	5	3	1	10	8	6	4	2
10	10	9	8	7	6	5	4	3	2	1

Les zéros ont été mis en rouge. Pouvez-vous comparer le nombre de zéros avec le nombre de facteurs premiers de 11 ?

Inverses et diviseurs de zéro

Existence d'un inverse pour la multiplication
Exemples
Diviseurs de 0
Cas où n est premier

Existence d'un inverse pour la multiplication

Théorème : Soit un entier a premier à n. Alors a est inversible dans

/ n

, c'est-à-dire qu'il existe b tel que

a b

1 mod n .

En fait, il s'agit d'une équivalence :

Théorème : Soit un entier a. Alors a est inversible dans si et seulement si a est premier à n.

La démonstration donne aussi un moyen de calcul de cet inverse.

L'entier a est premier avec n si et seulement s'il existe u et v dans

tels que

ua + vn = 1

Donc,

si a est premier avec n, il existe un entier u tel que u a = 1 mod n et a est inversible dans / n.
Si a est inversible dans / n, il existe un entier u tel que . Par définition de la congruence, cela signifie qu'il existe un entier v tel que u a - 1 = v n et on a u a + u v = 1, donc a et n sont premiers entre eux.

Exemple : Prenons n = 7 :

a = 0	0 1 mod 7
a = 1	1 1 mod 7
a = 2	2 1 mod 7
a = 3	3 1 mod 7
a = 4	4 1 mod 7
a = 5	5 1 mod 7
a = 6	6 1 mod 7

Exercice : Inverse : 1 2 3 Division : I II III

Exemples

Exemple: Prenons n = 6 :

a=0
a=1
a=2
a=3
a=4
a=5

Lorsque a n'a pas d'inverse, on voit qu'il est alors diviseur de zéro, c'est-à-dire que

pour un entier b.

Exemple : Pour n = 36

a=0		a=18
a=1		a=19
a=2		a=20
a=3		a=21
a=4		a=22
a=5		a=23
a=6		a=24
a=7		a=25
a=8		a=26
a=9		a=27
a=10		a=28
a=11		a=29
a=12		a=30
a=13		a=31
a=14		a=32
a=15		a=33
a=16		a=34
a=17		a=35

Cas où n est premier

Théorème. Si n = p est un nombre premier, tout nombre non nul dans a un inverse.

Démonstration Comme p est premier, il est premier avec tout nombre qu'il ne divise pas, c'est-à-dire avec tout nombre dont la classe de congruence modulo p n'est pas nul. On applique alors le théorème.

Théorème : Soit un entier a. Alors a est inversible dans si et seulement si a est premier à n.

Exercices : Puissance Calcul de puissances : I II

Diviseurs de 0

Lorsque a n'a pas d'inverse, on voit qu'il est alors diviseur de zéro, c'est-à-dire que

a times b equiv 0 mod n pour un entier b.

Proposition : Dans

/ n

, a est un diviseur de zéro si et seulement si a n'est pas premier avec n.

Démonstration.

Si a est diviseur de zéro, il n'est pas inversible donc d'après le théorème,
Théorème : Soit un entier a. Alors a est inversible dans si et seulement si a est premier à n.
il n'est pas premier avec n.
Si a n'est pas premier avec n, soit d le pgcd de a et de n. Soit b le quotient de n par d; on a
a = d a' , n = d b et ab = d a'b = n a'.
Donc a b = 0 mod n. La classe de b modulo n est non nulle, car b est un diviseur strict de n.

Exemple : Pour n = 20

a = 0	0 0 mod 20	a = 10	10 0 mod 20
a = 1	1 1 mod 20	a = 11	11 1 mod 20
a = 2	2 0 mod 20	a = 12	12 0 mod 20
a = 3	3 1 mod 20	a = 13	13 1 mod 20
a = 4	4 0 mod 20	a = 14	14 0 mod 20
a = 5	5 0 mod 20	a = 15	15 0 mod 20
a = 6	6 0 mod 20	a = 16	16 0 mod 20
a = 7	7 1 mod 20	a = 17	17 1 mod 20
a = 8	8 0 mod 20	a = 18	18 0 mod 20
a = 9	9 1 mod 20	a = 19	19 1 mod 20

Exercice : Diviseurs de zéro 1 2 3

Résolution de quelques problèmes

Résolution de l'équation linéaire a x = b mod n
Equation diophantienne linéaire à 3 inconnues
Petit théorème de Fermat
Résolution d'équations du type a^b=c mod n
Pour aller plus loin

Résolution de l'équation linéaire a x = b mod n

La question est de trouver tous les entiers x vérifiant l'équation

a x equiv b mod n

On peut adopter plusieurs points de vue selon qu'on est à l'aise ou non dans l'anneau

/ n

.
Première étape :

L'équation ax equiv

b mod n a une solution si et seulement si le pgcd d de a et de n divise b.

Dans ce cas, on divise l'équation par d (y compris n) et on est ramené au cas où a et n sont premiers entre eux.

Deuxième étape :

Première méthode : travailler dans Z
il s'agit de trouver les entiers x tels qu'il existe un entier k vérifiant
a x = b + k n
ou encore
a x - k n = b
On s'est donc ramené à résoudre une équation de Bezout. Elle a une solution car on a supposé que a et n sont premiers entre eux.
Deuxième méthode : travailler dans Z/nZ
Comme a et n sont premiers entre eux, il existe u et v tel que u a + v n = 1. En particulier, il existe un entier u tel que ua 1 mod n. On multiplie l'équation ax b mod n par u, ce qui donne
uax ub mod n
et donc comme ua 1 mod n
x ub mod n
et on a résolu le problème.

On se rend compte qu'en fait il s'agit de la démonstration de ce que a est inversible dans / n et que si ua + vn = 1, u mod n est l'inverse de a mod n dans / n.

L'avantage sur la première méthode : on n'a pas besoin de demander l'existence de k tel que ... Il est caché dans le a mod n : on se souvient que a mod n signifie en fait .

Exercices rapides : Equation linéaire modulaire

Exercice : Equation linéaire

Petit théorème de Fermat

Théorème Soit p un nombre premier impair. Alors pour tout entier n,

n^p

n mod p.

On en déduit le théorème de Fermat :

Théorème : Soit p un nombre premier impair. Alors pour tout entier n premier à p,

n^p-1

1 mod p.

Théorème Soit p un nombre premier impair. Soit n un entier premier à p. Alors,

il existe un plus petit entier r > 0 tel que n^r 1 mod p cet entier est un diviseur de p - 1 ;
les entiers s vérifiant n^s 1 mod p sont exactement les multiples de r.

Par le petit théorème de Fermat, l'ensemble des entiers r strictement positifs vérifiant n^r equiv

1 mod p est non vide car il contient p - 1. Il admet donc un plus petit élément. Notons-le r₀. Faisons la division euclidienne de p - 1 par r₀ : p - 1 = q r₀ + s avec s entier positif < r₀. On a

n^{p - 1}

(n^r₀)^q n^s mod p

d'où

n^s mod p

Donc, par minimalité de r₀, s est soit plus grand que r₀, soit nul. Donc s est nul, et r₀ divise p - 1.

Résolution d'équations du type a^b=c mod n

Il faut quand même préciser qui est l'inconnue ! Cela peut être a ou b.
On prend n = p un nombre premier.

Les équations du type a^x 1 mod p peuvent être traitées en utilisant le Théorème de Fermat
Théorème : Soit p un nombre premier impair. Alors pour tout entier n premier à p,

n^p-1 1 mod p.

et ses conséquences : Les solutions de cette équation sont les multiples d'un diviseur de p - 1 à trouver. On prend donc tous les diviseurs de p - 1 et on les essaye ! (on peut quand même réfléchir au moyen de ne pas faire trop de calculs : si a¹⁰ n'est pas congru à 1 modulo p, pas la peine d'essayer a² ou a⁵ ).
Les équations du type x^a b mod p avec a premier à p-1 et b premier à p : on va utiliser là encore le fait que x^{p - 1} 1 mod p. Pour cela, comme a et p - 1 sont premiers entre eux, on calcule l'identité de Bezout associée :
ua + v(p - 1) = 1
On a
b^u x^ua x mod p
et on a résolu l'équation.

Exercice : Equation multiplicative

Exercice : Equation multiplicative II

Equation diophantienne linéaire à 3 inconnues

Soient a, b, c et d quatre entiers. On désire résoudre l'équation

a x + b y + c z = d

en entiers. Les étapes de résolution peuvent être les suivantes :

Etape 1 : se ramener au cas où (a , b , c) sont premiers entre eux :
Explication
On commence par calculer le pgcd pgcd(a , b, c) des entiers (a , b , c). L'équation a une solution si et seulement si d divise pgcd(a, b, c). Dans ce cas, on peut diviser tous les coefficients par cet entier, ce qui nous ramène au cas où ce pgcd est 1.
Etape 2 : Lorsque a, b, c sont premiers entre eux, on se ramène au cas où deux des coefficients sont premiers entre eux : Explication
Soit r le pgcd de a et b . On pose a = r a₁, b = r b₁ avec a₁ et b₁ premiers entre eux.
Si (x , y , z) est une solution de l'équation, on a
cz d mod r .
Comme r et c sont premiers entre eux, il existe un entier u tel que u c 1 mod r et la congruence est équivalente à
z u d mod r
Ainsi, si on choisit u₁ un représentant de ud mod r , on a
u₁ c u c d d mod r
et
z = u₁ + r z₁
avec z₁ .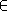
On pose d - u₁ c = d₁ r avec d₁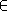 . L'équation devient
r a₁ x + r b₁ y + r c z₁ = d - u₁ c
c'est-à-dire
a₁ x + b₁ y + c z₁ = d₁
avec maintenant a₁ et b₁ premiers entre eux.
Etape 3 : Supposons a et b premiers entre eux. On cherche (et trouve) une solution particulière avec z = 0, ce qui revient à résoudre l'équation a x + b y = d :
Explication
Pour cela, on calcule des entiers u et v tels que a u + b v = 1 par l'algorithme d'Euclide. Une solution particulière est alors donnée par
x₀ = u d, y₀ = v d, z₀ = 0.
Etape 4 : Supposons a et b premiers entre eux. On cherche les solutions de l'équation
a x + b y + c z = 0 .
Explication
L'équation est équivalente à
a x + b y = -c z
La discussion dans le cas de deux variables (en considérant z comme fixé) implique que si u et v sont des entiers tels que a u + b v = 1, x et y s'écrivent sous la forme
x = -u c z + b j, y = -v c z - a j
c'est-à-dire matriciellement
Etape 5 : Supposons a et b premiers entre eux et au + bv = 1. La solution générale de l'équation a x + b y + c z = d est donnée de manière matricielle par :

avec j et k appartenant à .

Une équation diophantienne non linéaire sans solution

On désire montrer que l'équation x²+ y³= 7 n'a pas de solutions entières.

Soit p un nombre premier impair. Montrer que si l'équation x²+ 1 0 mod p a une solution, alors p est congru à 1 mod 4.
Solution
Ici, p est impair, donc p - 1 est divisible par 2.
Si -1 a² mod p, alors

a^{p - 1} 1 mod p.
La dernière congruence est le petit théorème de Fermat.
Théorème : Soit p un nombre premier impair. Alors pour tout entier n premier à p,

n^p-1 1 mod p.

Donc est pair, ce qui signifie que p 1 mod 4.
Supposons qu'il existe des entiers x et y tels que x²+ y³= 7.
- Montrer que y est impair.
  Solution
  Si y est pair, x² 7 mod 8, ce qui est impossible car tout carré est pair ou congru à 1 mod 8.
- Montrer que le produit d'entiers congrus à 1 mod 4 est congru à 1 mod 4.
  Solution
  Si les nombres a₁, ... , a_n sont congrus à 1 mod 4, on a
  a₁ ... a_n 1 ... 1 = 1 mod 4.
- Factoriser 8 - y³ sous la forme (2 - y) B. Montrer qu'il existe un nombre premier p congru à 3 mod 4 divisant B. En déduire qu'il existe un nombre premier congru à 3 mod 4 et divisant x²+ 1.
  Solution
  On a 8 - y³= (2 - y)(4 + 2y + y²), donc B = 4 + 2y + y². Comme y est impair,
  y² 1 mod 8, 2y 2 mod 4,
  donc B est congru à 3 mod 4. D'après la question précédente, il existe un nombre premier p divisant B et congru à 3 mod 4. Comme il divise B, il divise aussi (2 - y) B = 8 - y³= x²+ 1.
Conclure.
Solution
Soit des entiers x et y tels que x²+ y³= 7. On a trouvé un nombre premier p divisant y³- 8 et congru à 3 mod 4. Pour ce nombre premier,
x²+ 1 = 8 - y³ 0 mod p.
Donc -1 est un carré modulo p, ce qui est absurde, car p est congru à 3 mod 4.

Pour aller plus loin

Systèmes linéaires :
Exercices : Systèmes linéaires modulaires I II III
Racines de l'unité dans / p :
Exercices : I II III
Racine d'un polynôme :
Exercice : Relèvement
Authentification :
Exercice : Authentification
Exercices sur l'identité de Bezout :
Exercices : I II III IV
Critères de divisibilité
Exercices : I II III
Algorithme d'exponentiation
Exercices : Nombre de multiplications Exercice sur l'exponentiation
Logarithme discret
Exercices : Log discret I Log discret I
Factorisation par la méthode de Pollard
Méthode de cryptologie
Exercices : RSA I RSA analyse RSA création RSA décryptage Diffie-Hellman I Diffie-Hellman I

document sur les classes de congruence.
: group_theory,modular_arithmetic, interactive mathematics, interactive math, server side interactivity

Veuillez noter que les pages WIMS sont générées interactivement; elles ne sont pas des fichiers HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE. Il est inutile pour vous de les ramasser par un programme robot.

	1	2	3	4	5	6	7	8	9	10
0	0	0	0	0	0	0	0	0	0	0
1	1	2	3	4	5	6	7	8	9	10
2	2	4	6	8	10	1	3	5	7	9
3	3	6	9	1	4	7	10	2	5	8
4	4	8	1	5	9	2	6	10	3	7
5	5	10	4	9	3	8	2	7	1	6
6	6	1	7	2	8	3	9	4	10	5
7	7	3	10	6	2	9	5	1	8	4
8	8	5	2	10	7	4	1	9	6	3
9	9	7	5	3	1	10	8	6	4	2
10	10	9	8	7	6	5	4	3	2	1

	1	2	3	4	5	6	7	8	9	10
0	0	0	0	0	0	0	0	0	0	0
1	1	2	3	4	5	6	7	8	9	10
2	2	4	6	8	10	1	3	5	7	9
3	3	6	9	1	4	7	10	2	5	8
4	4	8	1	5	9	2	6	10	3	7
5	5	10	4	9	3	8	2	7	1	6
6	6	1	7	2	8	3	9	4	10	5
7	7	3	10	6	2	9	5	1	8	4
8	8	5	2	10	7	4	1	9	6	3
9	9	7	5	3	1	10	8	6	4	2
10	10	9	8	7	6	5	4	3	2	1

	1	2	3	4	5	6	7	8	9	10
0	0	0	0	0	0	0	0	0	0	0
1	1	2	3	4	5	6	7	8	9	10
2	2	4	6	8	10	1	3	5	7	9
3	3	6	9	1	4	7	10	2	5	8
4	4	8	1	5	9	2	6	10	3	7
5	5	10	4	9	3	8	2	7	1	6
6	6	1	7	2	8	3	9	4	10	5
7	7	3	10	6	2	9	5	1	8	4
8	8	5	2	10	7	4	1	9	6	3
9	9	7	5	3	1	10	8	6	4	2
10	10	9	8	7	6	5	4	3	2	1