Algèbre linéaire : espaces vectoriels
Objectifs et conseils
Avec ce chapitre, nous posons les bases de l'algèbre linéaire. Pour entrer au mieux dans ces définitions un peu abstraites, faites des dessins en dimension 2 ou 3. Vérifiez les propriétés énoncées sur des exemples simples. Prenez le temps d'assimiler les premières notions, vous comprendrez mieux la suite.Sommaire
Bibliographie
Les rappels de cours de cette partie sont issus des résumés de cours du S1 MIAS rédigés par Myriam Déchamps.
Introduction
Problèmes linéaires
On dira (on verra dans la suite une définition plus précise) que
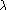 u,
où
u,
où
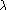 est un nombre réel ou complexe, sont aussi solutions du
problème.
est un nombre réel ou complexe, sont aussi solutions du
problème. En mathématiques, l'axiomatisation des problèmes linéaires se fait par la définition de la structure d'espace vectoriel et notre premier souci sera de distinguer, parmi les ensembles qui nous sont familiers, ceux qui peuvent être munis de cette structure.
Vecteurs : langage géométrique, langage algébrique
Soit un repère de l'espace. Soient M et M' deux points de l'espace, de coordonnées (a,b,c) et (a',b',c') dans ce repère. Alors les vecteurs et s'écrivent :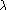 et ces opérations géométriques sur les
vecteurs se traduisent par des opérations algébriques sur leurs
coodonnées par rapport au repère fixé :
et ces opérations géométriques sur les
vecteurs se traduisent par des opérations algébriques sur leurs
coodonnées par rapport au repère fixé :
| Vecteurs | 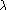
| |||
|---|---|---|---|---|
| Coordonnées | (a,b,c) | (a',b',c') | (a+a',b+b',c+c') |
Si nous ne retenons que l'aspect algébrique, il est alors possible de considérer des "vecteurs'' avec n coordonnées et de définir leur somme et le produit d'un vecteur par un nombre réel, de façon analogue.
Vecteurs dans Rn
Soit , convenons d'appeler vecteurs les éléments de (le produit cartésien usuel , n fois) et d'appeler scalaires les éléments de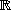 .
.
- la somme des vecteurs
u et
v est le vecteur
.
-
le produit du scalaire
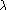 par le vecteur
u
est le vecteur
.
par le vecteur
u
est le vecteur
.
Cette définition va nous permettre de définir deux opérations dans .
- Addition : .
- Multiplication par un scalaire : .
Conclusion
Il y a bien d'autres ensembles E en mathématiques pour lesquels on sait additionner deux éléments et multiplier un élément par un nombre réel (resp. complexe), tout en restant dans E : par exemple,-
l'ensemble des fonctions de
dans
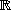
- l'ensemble des polynômes à coefficients complexes.
On s'aperçoit que des nombreux calculs ou preuves faits dans n'utilisent pas le fait que l'on travaille avec des coordonnées et sont valables lorsqu'on travaille dans les espaces de fonctions ou polynômes ci-dessus. Ces règles de calcul vont alors constituer la base de l'algèbre linéaire abstraite.
La démarche d'axiomatisation consiste à "oublier" la nature des éléments des ensembles E que l'on étudie pour ne retenir que le fait suivant : ils sont munis de deux opérations et ces opérations ont un certain nombre de propriétés.
On s'intéressera ensuite à établir les résultats qui découlent de cette structure algébrique et qui seront valables indépendamment de la nature des éléments de E. Ces éléments seront toujours appelés vecteurs, par commodité et pour favoriser l'intuition géométrique ; mais ce langage peut être déroutant : en tant qu'élément d'un espace vectoriel, une fonction est un vecteur !
- Tir de vecteurs avec deux vecteurs ,
- Tir avec trois vecteurs
Définition d'un espace vectoriel
-
Une loi de composition interne (c'est-à-dire, une application
),
appelée addition et notée
, vérifiant, pour tous
u,
v et
w dans
E :
- .
- .
- Il existe un élément de E appelé élément neutre et noté 0E tel que pour tout u dans E, .
- Pour tout u dans E, il existe un élément de E appelé opposé de u et noté -u, tel que .
-
Une loi de composition externe (c'est-à-dire, une application
), appelée
multiplication par un scalaire et notée
, vérifiant,
pour tous
u et
v dans
E et tous
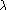 et
et
 dans
K :
dans
K :
- .
- .
- .
- Pour tout x dans E, .
Exemples
Un espace vectoriel sur K est aussi appelé un K-espace vectoriel, en abrégé K-ev. Les éléments de E sont appelés vecteurs.Un K-espace vectoriel E, muni de son addition, est un groupe commutatif, grâce aux propriétés 1. à 4.
Nous notons provisoirement les opérations d'un K-espace vectoriel par les symboles et , pour les différencier des opérations du corps des scalaires K et mieux comprendre les premiers exemples d'espaces vectoriels. Ensuite nous utiliserons les notations usuelles + pour l'addition et ou rien de tout pour la multiplication par un scalaire (ne pas oublier que l'on ne multiplie pas de vecteurs entre eux !).
- E=Kn ( ou , ) est un K-espace vectoriel.
-
E=
est un
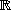 -espace vectoriel. Plus généralement, tout
-espace vectoriel. Plus généralement, tout
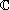 -espace vectoriel est un
-espace vectoriel est un
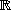 -espace vectoriel.
-espace vectoriel.
- E=K[X] est un K-espace vectoriel.
- L'ensemble des suites infinies d'éléments de K est un K-espace vectoriel.
- Soient A et l'ensemble des applications de A dans K. Alors E est un K-espace vectoriel. Cas particuliers : , , ou .
Règles de calcul
- .
- .
- .
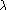 et
et
 dans
K. On a :
dans
K. On a :
- .
- .
- et .
- ;
- en particulier,
Combinaisons linéaires et systèmes linéaires
Dans , chercher à écrire le vecteur b comme combinaison linéaire de vecteurs donnés , c'est résoudre l'équation vectorielle : et
et
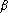 deux paramètres réels,
u1=(1,2,-3),
u2=(2,3,-4),
et
quatre
vecteurs de
. Le vecteur
b est-il combinaison linéaire des
vecteurs
u1,u2 et
u3 ?
deux paramètres réels,
u1=(1,2,-3),
u2=(2,3,-4),
et
quatre
vecteurs de
. Le vecteur
b est-il combinaison linéaire des
vecteurs
u1,u2 et
u3 ?
Cette question revient à savoir s'il existe tel que
- si , la solution du système est unique b s'écrit, pour tout , de facon unique, comme c.l. de u1,u2 et u3 ;
- Si et , le système n'a pas de solution donc b ne peut s'écrire comme combinaison linéaire de u1,u2 et u3 ;
- Si et , le système a une infinité de solutions et b s'écrit d'une infinité de fac cons comme c.l. de u1,u2 et u3.
On peut retenir de cet exemple que si on se donne trois vecteurs de et un vecteur b, il n'est pas toujours possible d'écrire b comme combinaison linéaire de ces trois vecteurs et que lorsque c'est possible, l'écriture n'est pas toujours unique.
Interprétation
On a vu ( par exemple ) que chercher à écrire b comme combinaison linéaire de n vecteurs u1, u2, un conduit à résoudre un système linéaire. Nous pouvons dire maintenant que le système a une solution, c'est-à-dire que b est combinaison linéaire de n vecteurs u1,u2, ..., un si et seulement si b appartient au sous-espace vectoriel engendré par les vecteurs u1,u2, ..., un.L'écriture peut être unique ou non. Cette propriété depend du rang du système . Elle décrit une propriété de l'ensemble des vecteurs u1,u2,...,un que nous verrons plus tard.
Sous-espaces vectoriels
Il est naturel de s'intéresser aux sous-ensembles d'un K-espace vectoriel qui sont, eux-mêmes, des espaces vectoriels. Il y a plusieurs façons équivalentes de les définir.- ;
- Pour tous u et v dans F, .
- Pour tous et , .
Exemples de sous-espaces vectoriels
Remarque. Le plus souvent, pour démontrer qu'un ensemble F est un K-espace vectoriel, on montre qu'il est un sous-espace vectoriel d'un espace vectoriel déjà connu (par exemple, un des sept espaces de la liste donnée au paragraphe précédent).-
Exemples triviaux
Soit E un K-espace vectoriel. Alors et E sont des sous-espaces vectoriels vectoriels de E, appelés les sous-espaces vectoriels triviaux de E.
-
Exemple du plan
Soient a, b et c trois nombres réels et . Alors F est un sev de si et seulement si c=0. Si l'on identifie au plan usuel muni d'un repère et si a et b ne sont pas tous deux nuls, a x+b y=c est l'équation d'une droite du plan : cette droite est un sev de si et seulement si elle passe par l'origine ; remarquons que si c=0 l'on a , où (b,-a) est un vecteur non nul de qui appartient à F.
-
Exemple des suites
L'ensemble des suites réelles convergentes est un sev du K-ev de toutes les suites à valeurs dans K.
-
Exemple des fonctions
F={ continue} est un sev de .
-
Exemple des polynômes
Soit , alors est un sev de K[X].
- Sur les axiomes de sous-espaces vectoriels
- Sur les axiomes de sous-espaces vectoriels dans l'espace des matrices
- Sur les axiomes de sous-espaces vectoriels dans l'espace des polynômes
Ensemble des solutions d'un système linéaire
Revenons sur les systèmes linéaires en utilisant les notions d'algèbre linéaire : l'ensemble des solutions d'un système linéaire homogène n'est jamais vide (il contient le n-uplet nul), est stable par addtion et par multiplication par un scalaire. Nous pouvons dire maintenant queRemarquons aussi que chaque équation du système définit un sous-espace vectoriel ; notons le sous-espace vectoriel (c'est un hyperplan vectoriel) de défini par la i-ième équation :
On a vu que l'ensemble des solutions d'un système linéaire homogène dépendait de n-r paramètres. Nous pouvons dire maintenant qu'il est engendré par n-r solutions particulières.
L'ensemble des solutions d'un système linéaire qui se présente comme la somme d'une solution particulière et du sous-espace vectoriel , ensemble des solutions d'un système linéaire homogène associé est appelé sous-espace affine.
Histoire
L'idée d'utiliser des couples ou de triplets de nombres pour localiser des points dans le plan ou dans l'espace a été clairement explicitée au milieu du 17e siècle.
A la fin du 19e siècle, mathématiciens et physiciens ont réalisé qu'il n'était pas nécessaire de se limiter à des triplets : des quadruplets (a,b,c,d) de nombres réels pouvaient être "vus" comme points dans un espace de "dimension 4" (ou des n-uplets de coordonnées comme des points en "dimension n"). Dès lors, le champ d'investigation de la géométrie s'élargit à la dimension n et on utilise davantage les outils algébriques en géométrie. Inversement, l'algèbre à n dimensions devient l'objet d'interprétations géométriques.
Mais notre visualisation géométrique ne s'étend pas au delà de
l'espace l'usuel, et même des "experts" raisonnent sur des "objets en dimension
n" par analogie avec des objets du plan ou de l'espace.
Une équation linéaire à
n inconnues
et à
coefficients
dans
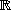 est une équation de la
forme
(lorsque
n=3 et
a1, a2
et
a3 ne sont pas tous nuls, cette équation est l'équation
cartésienne d'un plan de l'espace usuel). Il a existé des techniques
de résolution de systèmes d'équations linéaires dès l'antiquité, mais
ce n'est qu'à partir du milieu du 19e siècle que les systèmes
linéaires deviennent un objet d'étude et permettent de dégager les
premiers concepts théoriques liés à la linéarité : vecteur,
dépendance et indépendance linéaire (dans un texte de G. F. Frobenius
(1849-1917)).
est une équation de la
forme
(lorsque
n=3 et
a1, a2
et
a3 ne sont pas tous nuls, cette équation est l'équation
cartésienne d'un plan de l'espace usuel). Il a existé des techniques
de résolution de systèmes d'équations linéaires dès l'antiquité, mais
ce n'est qu'à partir du milieu du 19e siècle que les systèmes
linéaires deviennent un objet d'étude et permettent de dégager les
premiers concepts théoriques liés à la linéarité : vecteur,
dépendance et indépendance linéaire (dans un texte de G. F. Frobenius
(1849-1917)).
Les premières approches axiomatiques en algèbre linéaire datent de la fin des années 1880. Dans la période de 1890 à 1930 se développe l'étude des corps et des anneaux et l'ensemble de l'algèbre est reconstruit à partir d'une approche axiomatique des structures. Ce changement est enteriné par la publication par Van der Waerden en 1930-31 des deux tomes de son Moderne Algebra, qui est une compilation et une mise en forme des fondements de l'algèbre moderne ayant émergé les deux décennies précédentes. Ce livre devient un livre de référence pour plusieurs générations de mathématiciens. Dans la même période, la description des problèmes linéaires en termes de coordonnées, acquise à la fin du 19e siècle, évolue vers l'approche axiomatique actuelle. Cette approche axiomatique apparaît comme une volonté de donner de meilleurs fondements à l'ensemble des résultats sur l'algèbre linéaire et de permettre la modélisation de nouveaux problèmes.