On veut résoudre dans 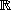 l'inéquation (I) :
.
l'inéquation (I) :
.
Résolvez (I) sur papier libre, en complétant les affirmations suivantes.
Réécrire sous la forme exp( ), où est un entier relatif.
Réécrire sous la forme exp( ) , où est une expression sans exponentielle.
Réécrire sous la forme exp( ).
On veut étudier en fonction de
le signe de :
.
Pour ce faire, on commence par résoudre l'inéquation
.
Résolvez l'inéquation sur papier libre puis complétez les affirmations suivantes.
On peut écrire l'équivalence suivante :
On appliquer car le deuxième membre de l'inéquation est .
On peut écrire l'équivalence suivante :
On peut appliquer , car le deuxième membre de l'inéquation est .
On peut écrire l'équivalence suivante :
On ne peut pas appliquer , car le deuxième membre de l'inéquation est .
En résolvant on obtient :
Posons . On dresse alors le tableau de signes suivant :
| 0 |
On veut résoudre dans 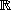 l'inéquation (I) :
.
l'inéquation (I) :
.
Résolvez (I) sur papier libre, en complétant les affirmations suivantes.
On peut écrire l'équivalence suivante :
(I)
On appliquer car le deuxième membre de (I) est .
On peut écrire l'équivalence suivante :
(I)
On peut appliquer , car le deuxième membre de (I) est .
On peut écrire l'équivalence suivante :
(I)
On ne peut pas appliquer , car le deuxième membre de (I) est .
On veut résoudre dans 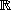 l'inéquation (I) :
.
l'inéquation (I) :
.
Résolvez (I) sur papier libre, puis complétez les affirmations suivantes.
Le premier membre de (I) est défini à condition que .
Le second membre de (I) est défini à condition que .
Pour tout réel vérifiant les conditions 1. et 2. , on a :
On en déduit que l'ensemble des solutions de (I) est
On veut résoudre dans 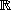 l'inéquation (I) :
.
l'inéquation (I) :
.
Résolvez (I) sur papier libre, puis complétez les affirmations suivantes.
Pour écrire vous devez entrer exp(a) ou e^(a).
Le premier membre de (I) est défini si et seulement si .
La condition 1. étant vérifiée, on peut écrire les équivalences suivantes :
(I) ln( )
(I)
L'ensemble des solutions de (I) est
On veut résoudre dans 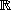 l'inéquation (I) :
.
l'inéquation (I) :
.
Résolvez (I) sur papier libre, puis écrivez son ensemble de solutions à l'aide des menus déroulants ci-dessous.
Pour écrire l'ensemble vide, saisir ] 0 , 0 [.
L'ensemble des solutions de (I) est l'intervalle :
Résoudre dans 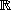 l'inéquation (I) :
.
l'inéquation (I) :
.
A quelle condition sur le premier membre de (I) est-il défini ?
A quelle condition sur le second membre de (I) est-il défini ?
Pour
vérifiant les conditions 1. et 2. , on peut simplifier (I) en une inéquation (I') du premier degré.
Poser l'inéquation (I'). Quelles sont les solutions de (I') ?
En déduire l'ensemble des solutions de (I).
(il faut tenir compte des conditions obtenues en 1., 2. et 3.)
ln( ) est défini à condition que , c'est à dire que .
Pour tout réel vérifiant ces deux conditions, on peut ramener (I) à une inéquation du premier degré en appliquant la règle
Les réels solutions de (I) doivent donc vérifier les trois inégalités :
Chaque inégalité définit un intervalle ; l'ensemble des solutions est l'intersection des trois intervalles.
| ∈ avec = |
| ∈ avec = |
| ∈ avec = |
solution de (I) si et seulement si
∈


|
Formons d'abord l'intersection des deux premiers intervalles :
 =
= Cet ensemble est vide, donc a fortiori l'intersection
est vide aussi.
Conclusion : L'inéquation (I) n'a aucune solution.
L'intersection de
avec
est vide.
Conclusion : L'inéquation (I) n'a aucune solution.
Formons ensuite l'intersection avec le troisième intervalle :
 =
= Conclusion : L'ensemble des solutions de (I) est .
Réécrire sous la forme ln( ), où est un nombre rationnel.
Réécrire comme le logarithme d'un produit :
On considère la suite géométrique (
) de premier terme
et de raison
.
On cherche pour quelles valeurs de l'entier
on a
.
Il s'agit donc de résoudre dans 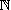 l'inéquation (I) :
l'inéquation (I) :
Résolvez (I) sur papier libre, puis complétez les affirmations suivantes.
La suite géométrique est et .
L'inéquation (I) équivaut à ln( ) / ln(q) .
Les solutions de l'inéquation (I) sont tous les entiers naturels à l'entier = .
On considère la fonction
définie par la formule
.
Faites-en l'étude sur papier libre, puis remplissez le questionnaire suivant.
est défini si et seulement si :
Soit l'ensemble de définition de . Parmi les ensembles suivants, lequel est ?
| = ] ; +∞ [ | = ] -∞ ; [ | = [ ; +∞ [ | = ] -∞ ; ] |
Pour tout réel appartenant à , on peut écrire :
Pour
, comme
est strictement positif,
est du signe de
.
Donc, sur l'ensemble
, on obtient que
Des variations de la fonction on déduit que :
On veut étudier en fonction de le signe de : .
Pour ce faire, on commence par regarder si ce signe peut être déterminé de manière immédiate.
On peut écrire les équivalences suivantes :
.
.
En résolvant on obtient :
Posons . On dresse alors le tableau de signes suivant :
| 0 |
L'expression est définie si , c'est à dire si appartient à l'intervalle .
On veut étudier dans le signe de l'expression : .
On doit donc résoudre l'inéquation
Compléter les étapes suivantes ; pour écrire vous devez entrer exp(a) ou e^(a).
Pour appartenant à , on peut écrire les équivalences suivantes :
> 0 ln( )
On en déduit le tableau de signes suivant :
| 0 |
L'expression est définie si , c'est à dire si appartient à l'intervalle .
On veut étudier dans le signe de l'expression : .
Résoudre sur papier libre l'inéquation puis compléter le tableau de signes.
Pour écrire vous devez entrer exp(a) ou e^(a).
| 0 |
Simplifier l'expression suivante sous forme d'un entier relatif.
Veuillez noter que les pages WIMS sont générées interactivement; elles ne sont pas des fichiers HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE. Il est inutile pour vous de les ramasser par un programme robot.